Inhaltsverzeichnis
1 Ziel des Wilcoxon-Test in SPSS
Der Wilcoxon-Test ist ein nicht parametrischer Mittelwertvergleich bei 2 abhängigen Stichproben. Er verwendet Ränge statt die tatsächlichen Werte und ist das Gegenstück zum t-Test bei abhängigen Stichproben, allerdings hat er nicht solche strengen Voraussetzungen.
2 Voraussetzungen des Wilcoxon-Test in SPSS
- zwei voneinander abhängige Stichproben/Gruppen
- ordinal oder metrisch skalierte y-Variable
- normalverteilte y-Variable innerhalb der Gruppen nicht nötig
3 Durchführung des Wilcoxon-Test in SPSS
Über das Menü in SPSS: Analysieren -> Nichtparametrische Test -> Alte Dialogfelder -> 2 verbundene Stichproben
Als Testpaare ist die zu testende Variable einzusetzen. Die Gruppierungsvariable ist die Variable, die die Gruppen unterscheidet. Im Beispiel testen wir den Ruhepuls vor Training (Variable 1) und den Ruhepuls nach 10 Wochen Training (Variable 2) auf Unterscheide hinsichtlich ihres Ruhepulses.
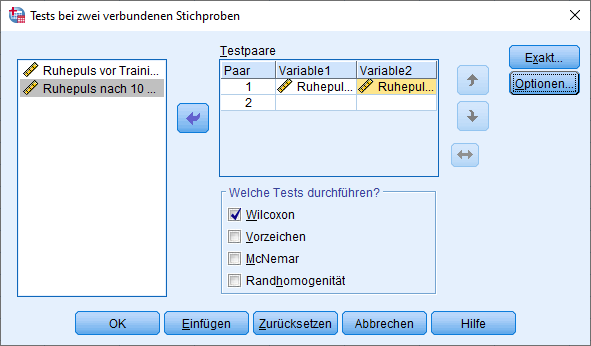
Als Test muss der Wilcoxon-Test ausgewählt werden. Zusätzlich sollte unter Optionen noch “Deskriptive Statistik” ausgewählt werden.
Ein Klick auf “OK” führt die Berechnung durch und zeigt die Ergebnisse an.
4 Interpretation des Wilcoxon-Test in SPSS
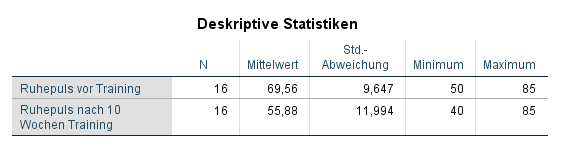
Die deskriptiven Statistiken geben lediglich einen kurzen Überblick, wie der Ruhepuls vor und nach dem 10-wöchigen Training ausgeprägt sind. Mittelwert, Standardabweichung, Minimum und Maximum werden angezeigt. Es ist erkennbar, dass der Ruhepuls im Mittel nach 10 Wochen geringer ist, was ein erstes Anzeichen ist, dass sich nach dem Training wohl eine Verringerung des Ruhepulses eingestellt hat. Diesen ersten Eindruck gilt es nachfolgend mit dem Wilcoxon-Test auf statistische Signifikanz zu testen. Die Standardabweichung ist etwas gestiegen, was auf eine breitere Streuung hindeutet.
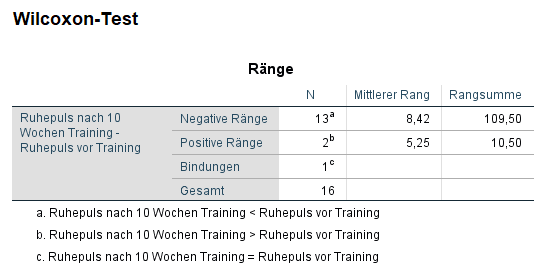
Der Wilcoxon-Test arbeitet mit Rängen. Bei negativen Rängen hat der Proband einen auf den Rang in der Stichprobe bezogen niedrigeren Ruhepuls. Positiv heißt ein höherer Rang und Bindung steht für keine Veränderung. Man kann also salopp sagen, dass bei 13 (= Negative Ränge) Personen eine Senkung des Ruhepulses eingetreten ist. Bei 2 (=Positive Ränge) gab es eine Erhöhung des Ruhepulses und bei 1 (= Bindungen) gab es keine Änderung. Allerdings ist hiermit noch nicht gesagt, ob es tatsächlich einen statistisch signifikanten Unterschied gibt. Hierzu braucht es den Wilcoxon-Test und dessen Ergebnisse. In SPSS ist die Ausgabe relativ karg.
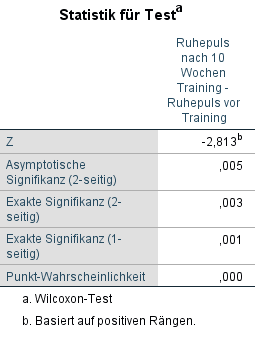
Die Tabelle zeigt in der zweiten Zeile die “Asymptotische Signifikanz (2-seitig)” von 0,005. Wenn die Stichprobe mindestens 25 Probanden umfasst, wird diese verwendet (Harris, T., & Hardin, J. W. (2013). Exact Wilcoxon signed-rank and Wilcoxon Mann–Whitney ranksum tests. S. 339). Bei weniger als 25 (hier 16) muss die exakte Signifikanz betrachtet werden! Die exakte Signifikanz (2-seitig) ist mit 0,003 kleiner als 0,05 und reicht zur Verwerfung der Nullhypothese von gleichen Ruhepulsen über die Zeitpunkte hinweg. Demzufolge wird die Alternativhypothese angenommen, dass über die Zeitpunkte hinweg (nach dem Training) unterschiedliche Ruhepulse existieren.
Achtung: Wenn bereits eine Wirkungsvermutung vor dem Test existiert – die plausible Annahme, dass ein 10-wöchiges Kardiotraining den Ruhepuls senkt, wäre so eine – dann würde man 1-seitig testen. Hierzu darf die Asymptotische bzw. Exakte Signifikanz halbiert werden und erneut mit 0,05 verglichen werden. In diesem Falle ändert sich entsprechend nichts an der Aussage der Verwerfung der Nullhypothese.
5 Ermittlung der Effektstärke des Wilcoxon-Tests
Die Effektstärke r wird mit folgender Formel berechnet. Der z-Wert wird durch die Wurzel der Stichprobengröße geteilt. Aufgrund der Betragsstriche wird dieser Quotient immer positiv sein.
![Rendered by QuickLaTeX.com \[ r = \lvert \frac{z}{\sqrt{N}}\rvert= \lvert \frac{-2,813}{\sqrt{16}} \rvert=0,7033\]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-bc8c8aa445b6e1bfce2e766a7f631293_l3.png)
Im Beispiel ist also -2,813 durch die Wurzel aus 16 zu teilen und der Betrag dessen zu nehmen. Das Ergebnis hieraus lautet: 0,7033. Laut Cohen: Statistical Power Analysis for the Behavioral Sciences (1988), S. 79-81 sind die Effektgrenzen 0,1-0,3 (schwach), 0,3-0,5 (mittel) und größer 0,5 (stark).
Im vorliegenden Beispiel ist die Effektstärke mit 0,7033>0,5 stark. Es handelt sich also um einen starken Effekt hinsichtlich des Unterschiedes des Ruhepulses vor und nach dem 10-wöchigen Training.
6 Tipp zum Schluss
Findest du die Tabellen von SPSS hässlich? Dann schau dir mal an, wie man mit wenigen Klicks die Tabellen in SPSS im APA-Standard ausgeben lassen kann.
7 Videotutorial


