Inhaltsverzeichnis
1 Ziel des Welch-Tests (Welch t-Test bei ungleichen Varianzen)
Der Welch-Test testet unabhängige Stichproben darauf, ob bei zwei unabhängigen Stichproben die Mittelwerte unterschiedlich sind. Allerdings benötigt der Welch-Test im Gegensatz zum normalen t-Test keine homogenen Varianzen. Das bedeutet, der Test funktioniert auch ohne in etwa ähnliche Varianzen der Gruppen. Die Durchführung und Interpretation zeigt dieser Artikel.
2 Voraussetzungen des Welch-Tests
Die wichtigsten Voraussetzungen sind:
- zwei voneinander unabhängige Stichproben/Gruppen
- metrisch skalierte y-Variable
- normalverteilte y-Variable innerhalb der Gruppen
- Keine homogene (nahezu gleiche) Varianzen der y-Variablen der Gruppen
- Optional: fehlende Werte definiere, fehlende Werte identifizieren und fehlende Werte ersetzen
Hinweis: Sind deine Varianzen homogen, rechnest du den einfachen t-Test bei unabhängigen Stichproben.
Fragen können unter dem verlinkten Video gerne auf YouTube gestellt werden.
3 Durchführung des Welch-Tests in SPSS
Zunächst ist für jede Gruppe die abhängige Variable auf Normalverteilung zu testen. Das zeigt dieser Artikel. Ist diese Voraussetzung nicht erfüllt, empfiehlt sich der Mann-Whitney-U-Test.
Ist diese Voraussetzung erfüllt, fahrt ihr hier fort:
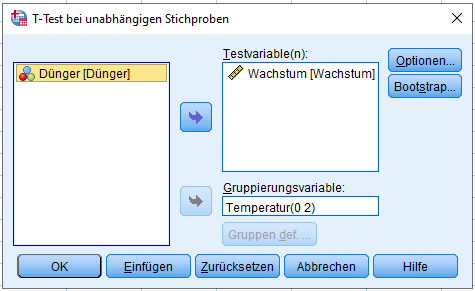
Über das Menü in SPSS: Analysieren -> Mittelwerte vergleichen -> T-Test für unabhängige Stichproben
Unter Optionen 95% Konfidenzintervall und “Fallausschluss Test für Test”.
Als Gruppierungsvariable ist das die beiden Gruppen trennende Merkmal/Variable auszuwählen und die beiden Gruppen anhand der Merkmalsausprägungen zu definieren. In meinem Beispiel teste ich Pflanzenwachstum in zwei unterschiedlichen Umgebungen. Eine sehr kalte Temperatur und eine normale Temperatur. Dies sind meine zwei Gruppen. Ich möchte mit dem Welch-Test herausfinden, ob sich die Gruppen hinsichtlich des Pflanzenwachstums signifikant voneinander unterscheiden.
4 Interpretation der Ergebnisse des Welch-Tests in SPSS
4.1 Deskriptive Statistiken
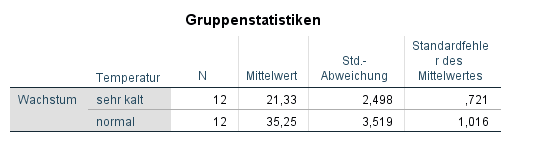
Ein erster Eindruck ist anhand der Tabelle der deskriptiven Statistiken erkennbar. Die Mittelwerte der abhängigen Variable (hier: Pflanzenwachstum) unterscheiden sich je nach Temperatur (sehr kalt, normal). Die Standardabweichungen (die Wurzel der Varianz) ist über die zwei Gruppen durchaus verschieden. Ein analytischer Test ist aber dennoch durchzuführen.
4.2 Varianzhomogenität
Varianzhomogenität wurde im “Levene-Test der Varianzgleichheit” geprüft. Ist der Wert unter 0,05, wird die Nullhypothese (Homogenität/Gleichheit der Varianzen) verworfen. Die Nullhypothese lautet hierbei, dass die Varianzen homogen sind.

Im Beispiel liegt die Signifikanz mit 0,014 unter 0,05. Somit wird die Nullhypothese von Varianzhomogenität verworfen. Demzufolge wird die Alternativhypothese heterogener Varianzen angenommen. Folglich sind die Ergebnisse des t-Tests mit ungleichen Varianzen zu interpretieren.
4.3 Welch-Test (der t-Test bei ungleichen Varianzen)
Da wir festgestellt haben, dass wir ungleiche Varianzen haben, kümmern wir uns nur um die Zeile “Varianzen sind nicht gleich“.

Hier müssen wir uns lediglich um die Spalte “Sig. (2-seitig)” kümmern. Wir erkennen, dass wir hier eine Signifikanz von 0,000 haben. Diese liegt unter dem typischen Alphafehler von 0,05. Wir verwerfen die Nullhypothese des Welch-Tests von Gleichheit der Mittelwerte der beiden Gruppen. Wir nehmen daher die Alternativhypothese an, dass sich die beiden Gruppen hinsichtlich des Mittelwertes unterscheiden. Es ist auch zu sehen, dass die Mittlere Differenz -13,917 ist. Diese ergibt sich aus dem Wachstum bei sehr kalter Temperatur (21,33) abzüglich des Wachstums bei normaler Temperatur (35,25).
Ein 1-seitiges testen ist möglich. Hierzu wird die Signifikanz schlicht halbiert. Das ändert in dem Falle allerdings nichts am Ergebnis.
ACHTUNG: Testet man einseitig, ist das im Vorfeld zu benennen.
5 Die Effektstärke – wie stark ist der Unterschied?
Effektstärken dienen zur Einordnung, wie stark sich die beiden Stichproben unterscheiden. Es gibt zwei mögliche Effektstärkemaße: Cohen’s d und Cohen’s r.
5.1 Cohen’s d
Die Effektstärke Cohen’s d ist die vorzuziehende Effektstärke. Cohen’s d wird von SPSS erst ab Version 27 ausgegeben. Hier zeige ich, wie man sie anfordert. In SPSS 26 oder früher muss man Cohen’s d manuell berechnen, was ich hier zeige.
5.2 Cohen’s r Cohen’s r ist weniger üblich. Dessen Berechnung erfolgt über die Formel mit t² als quadrierter T-Wert und df als degrees of freedom (Freiheitsgrade).
![Rendered by QuickLaTeX.com \[ r = \sqrt{\frac{t^2}{t^2+df}} \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-ea814ae95eca7b794de9e0f93fef19d1_l3.png)
Ab 0,1 ist es ein schwacher Effekt, ab 0,3 ein mittlerer und ab 0,5 ein starker Effekt.
Im Beispiel ist der t-Wert -11,169 und die Freiheitsgrade (df) 19,842. Eingesetzt in die Formel:
![Rendered by QuickLaTeX.com \[ r = \sqrt{\frac{(-11,169)^2}{(-11,169)^2+19,842}}= 0,929\]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-d9553a61b1210f40ce4c392dbfecf96e_l3.png)
Das Ergebnis von 0,929 liegt über der Grenze zum starken Effekt. Somit ist der Unterschied stark.
6 Berichten der Ergebnisse des Welch-Tests aus SPSS
Da es nicht viele Werte gibt, ist nicht viel zu berichten:
Das Schema ist folgendes: t(df) = T-Wert, p = Signifikanz
Das sieht im Beispiel so aus, da wir uns in der zweiten Zeile befinden: t(19,842) = -11,169; p < 0,001.
7 Videotutorials


