Inhaltsverzeichnis
1 Ziel der Welch-ANOVA
Die Welch-ANOVA testet unabhängige Stichproben darauf, ob bei mehr als zwei unabhängigen Stichproben die Mittelwerte unterschiedlich sind. Allerdings benötigt die Welch-ANOVA im Gegensatz zur normalen ANOVA keine homogenen Varianzen. Das bedeutet, der Test funktioniert auch ohne in etwa ähnliche Varianzen der Gruppen. Sind deine Varianzen homogen, rechnest du die einfache ANOVA hier. Ein kurzes Tutorial zur zweifaktoriellen Varianzanalyse ist hier zu finden.
2 Voraussetzungen der Welch-ANOVA
Die wichtigsten Voraussetzungen sind:
- mehr als zwei voneinander unabhängige Stichproben/Gruppen – bei nur zwei Gruppen ist der Welch-Test zu rechnen
- metrisch skalierte y-Variable
- normalverteilte Fehlerterme, ersatzweise normalverteilte y-Variable innerhalb der Gruppen
- Keine homogenen (nahezu gleiche) Varianzen der y-Variable über die Gruppen
3 Durchführung der Welch-ANOVA in SPSS
Über das Menü in SPSS:
Analysieren > Allgemeines lineares Modell > Univariat
ODER
Analysieren > Mittelwerte vergleichen > Einfaktorielle Varianzanalyse (*empfohlen)
Als Abhängige Variable ist die Testvariable auszuwählen. Als Faktor ist das die Gruppen trennende Merkmal/Variable auszuwählen. Im Beispiel prüfe ich den Ruhepuls auf Unterschiede über drei Gruppen hinweg.
Unter Optionen folgendes anhaken: Deskriptive Statistik, Test auf Homogenität der Varianzen und insbesondere Welch.
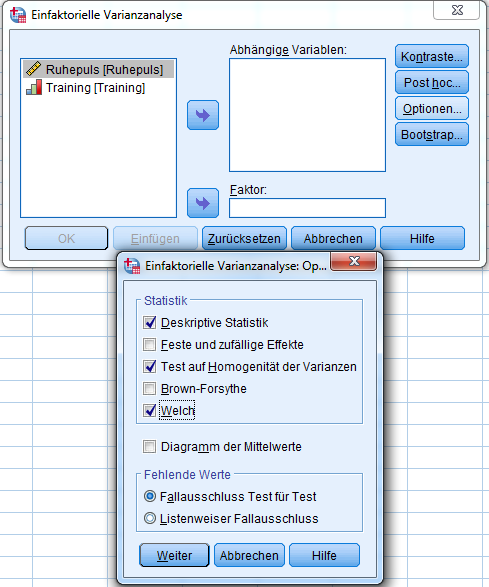
Post hoc dient dem mehrfachen paarweisen Vergleich zwischen den Gruppen. Ist also ein statistisch signifikanter Unterschied vorhanden, interessiert uns, zwischen welchen der mindestens drei Gruppen dieser besteht. Unter Post hoc kann “Bonferroni” angehakt werden, obwohl es bei “Varianzgleichheit angenommen” steht. Zum Hintergrund: post-Hoc-Tets sind t-Tests. Da mit mehrfachem Testen derselben Gruppen die Wahrscheinlichkeiten einen Alpha-Fehler (=fälschliches Ablehnen der Nullhypothese) zu begehen steigt, muss die Signifikanz korrigiert werden. Dazu dienen die vielen verschiedenen Korrekturverfahren. Da die Varianzen sehr wahrscheinlich nicht homogen sind, empfiehlt es sich bei “Keine Varianzgleichheit angenommen” “Dunnett-T3” und “Games-Howell” anzuhaken.
4 Interpretation der Ergebnisse der Welch-ANOVA in SPSS
4.1 Deskriptive Statistiken
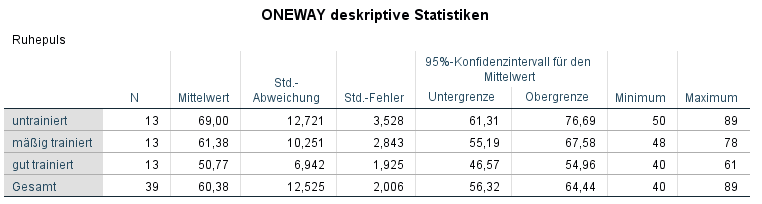
1. Ein erster Eindruck ist anhand der Tabelle der deskriptiven Statistiken erkennbar. Die Mittelwerte des abhängigen Variable (hier: Ruhepuls) nehmen mit dem Trainingsgrad (untrainiert, mäßig trainiert, gut trainiert) ab. Die Standardabweichungen (die Wurzel der Varianz) ist über die drei Gruppen durchaus verschieden. Ein analytischer Test ist aber dennoch durchzuführen.
4.2 Varianzhomogenität
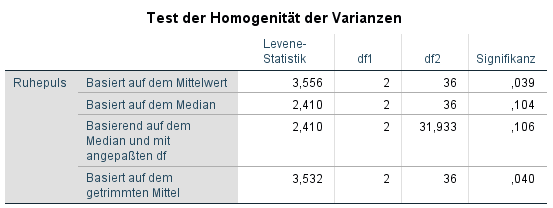
2. Die Varianzhomogenität wurde im “Test der Homogenität der Varianzen” mit dem sog. Levene-Test vorgenommen. Ist der p-Wert/Signifikanz unter 0,05, wird die Nullhypothese (Homogenität/Gleichheit der Varianzen) verworfen. Hier ist die Signifikanz in der ersten Zeile (Basiert auf dem Mittelwert) mit 0,039 < 0,05 gegeben. Das bedeutet, dass die Nullhypothese von Gleichheit der Varianzen verworfen werden muss. Zwar sind die Signifikanzen in den anderen Zeilen >0,05, ein konservativer Ansatz ist aber bereits bei so einem Ergebnis keine normale ANOVA, sondern stattdessen eine Welch-ANOVA zu rechnen.
4.3 Welch-ANOVA
3. Die Welch-ANOVA “versteckt” sich in der Tabelle “Robuste Testverfahren zur Prüfung auf Gleichheit der Mittelwerte”. Hierbei ist vor allem erneut die Signifikanz beachtenswert. Analog zur normalen ANVOA hat die Welch-ANOVA die Nullhypothese von Gleichheit der Mittelwerte über die Gruppen hinweg. Bei einem Signifikanzwert von <0,05 ist diese jedoch zu verwerfen. In diesem Beispiel wird die Nullhypothese verworfen und damit die Alternativhypothese angenommen: Ungleichheit der Mittelwerte über die Gruppen.

ACHTUNG: Ein 1-seitiges Testen ist nicht möglich, da bei mehr als zwei Gruppen nicht gesagt werden kann, welche Gruppe einen größeren oder kleineren Wert hat!
4.4 Post-Hoc-Tests
4. Die Tabelle “Post-Hoc-Tests” zeigt, ob statistisch signifikante Unterschiede zwischen den Gruppen existieren. Ist die Signifikanz der jeweiligen Paarung kleiner als 0,05, geht man von statistisch signifikanten Unterschieden hinsichtlich der Mittelwerte zwischen den zwei verglichenen Gruppen aus.
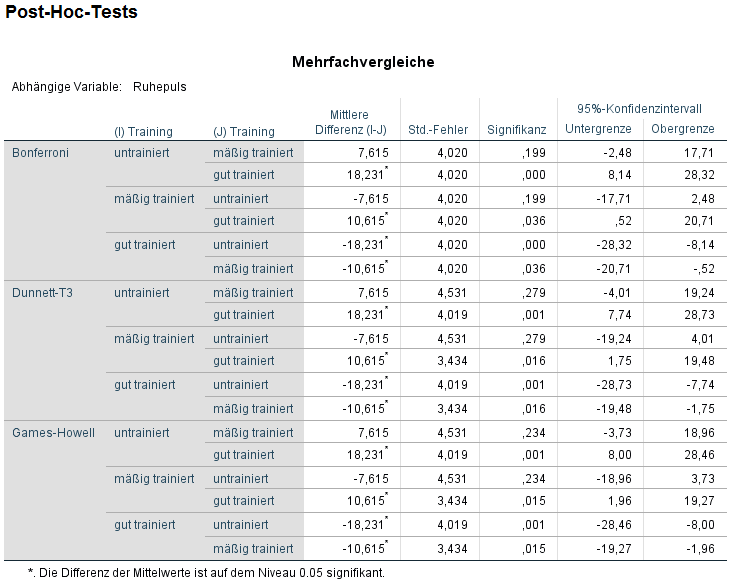
In obenstehender Tabelle gibt es drei Post-Hoc-Tests: Bonferroni, Dunnett-T3 und Games-Howell. In der zweiten Spalte steht die erste Gruppe und in der dritten Spalte die zweite Gruppe, mit der die erste verglichen wird. In der vierten Spalte steht die jeweilige mittlere Differenz, also die Differenz der Gruppenmittelwerte. In der sechsten Spalte stehen die Signifikanzen. Auch hier gilt: wenn die Signifikanz <0,05 ist, wird die Nullhypothese von Gleichheit der Mittelwerte für den jeweiligen paarweisen Vergleich abgelehnt.
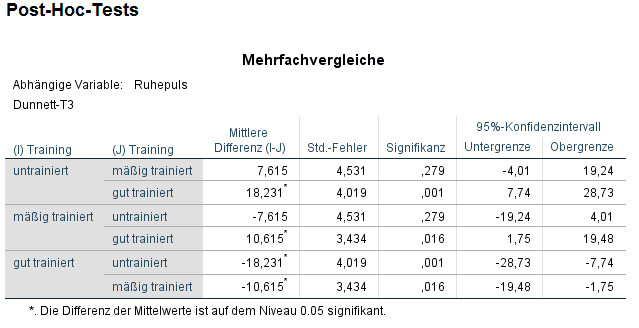
Speziell für den Dunnett-T3-Post-Hoc-Test erkennt man, dass untrainiert und mäßig trainiert bei einer mittleren Differenz von 7,615 mit einer Signifikanz von 0,279 keine Unterschiede zu haben scheinen. Untrainierte und gut Trainierte haben bei einer mittleren Differenz und einer Signifikanz von 0,001 allerdings scheinbar einen Unterschied in ihren Mittelwerten. Schließlich haben mäßig und gut trainierte eine mittlere Differenz von 10,615 mit einer Signifikanz von 0,016. Auch zwischen ihnen scheint es Unterschiede beim Mittelwert des Ruhepulses zu geben.
5 Videotutorial
6 Tipp zum Schluss
Findest du die Tabellen von SPSS hässlich? Dann schau dir mal an, wie man mit wenigen Klicks die Tabellen in SPSS im APA-Standard ausgeben lassen kann.


