Variationskoeffizient in SPSS berechnen

Der Variationskoeffizient ist ein relatives Streumaß. Relativ bedeutet, er hängt nicht vom Wertebereich der zu beurteilenden Variable ab. Somit ist er für den Vergleich von Variablen mit unterschiedlichen Wertebereichen geeignet – im Gegensatz zu Standardabweichung und Varianz.
 

1 Variationskoeffizient für das wide-Format in SPSS berechnen

1.1 Datengrundlage

In SPSS gibt es die Möglichkeit den Variationskoeffizienten zu berechnen nur für das sog. Wide-Format. Das heißt, dass bspw. ein Proband zu mehreren Zeitpunkten für denselben Parameter (Gewicht, Ruhepuls,…= vermessen wird. Innerhalb dessen kann nun die Streuung der Werte berechnet werden. Entweder ganz klassisch mit der Standardabweichung (oder der Varianz) oder eben adjustiert um den Wertebereich. Warum ist das wichtig? Hierzu ein kleines Beispiel:

Proband	Wert in t0	Wert in t5	Wert in t10	Standardabw.	Mittelwert	Variationskoef.
1	166	153	171	9,29	163,33	0,06
2	56	56	62	3,46	58	0,06

Es ist erkennbar, dass beide Probanden schwankende Werte aufweisen. Die Schwankung wird mit der Standardabweichung erfasst und beträgt für den ersten Probanden 9,29. Für den zweiten Probanden sind es lediglich 3,46. Bedeutet das, dass der zweite Proband eine geringere Schwankung in seiner Messreihe hat? Nein, da die Standardabweichung nur deswegen beim ersten Proband vergleichsweise so hoch ist, weil die Werte um etwa 100 größer sind. Die relative Streuung mittels des Variationskoeffizienten weist bei beiden Probanden den gleichen Wert auf. Es wurde um den Wertebereich korrigiert. Statt eines absoluten Streumaßes findet ein relatives Streumaß Anwendung.

 

1.2 Variationskoeffizient berechnen

Für den Fall des wide-Formats gibt es zwei Möglichkeiten, die ich zeigen werde. Zum einen die in SPSS hinterlegte Formel, zum anderen die manuelle Berechnung.

 

1.2.1 SPSS-Funktion

Über Transformieren -> Variable berechnen

 

1. Als erstes ist im Bereich Funktionsgruppe “Alle” auszuwählen.
2. Danach ist “Cfvar” bei Funktionen und Sondervariablen zu suchen und zu selektieren.
3. Dann sind die Ausprägungen zu den Messzeitpunkten (=Variablen) in den numerischen Ausdruck zu schreiben. Der Variablenname ist hier zu verwenden und jeweils mit Komma zu trennen. Ein Doppelklick auf die Variablen reicht hierfür auch aus.
4. Zuletzt ist noch die neue Zielvariable zu benennen. Die Benennung ist frei wählbar, sollte aber dem Kontext entsprechen. Ich habe hier “Varkoef” gewählt.

 

Ein Klick auf OK führt dann zur Berechnung des Variationskoeffizienten. In der Datenansicht erscheint nun die neue Variable “Varkeof”:

---

 

1.2.2 Manuelle Berechnung

Auch hier geht es zunächst über Transformieren -> Variable berechnen.

 

Als Nächstes muss man wissen, dass sich der Variationskoeffizient wie folgt berechnet:

   

Demzufolge kann man die SD-Funktion und Mean-Funktion direkt miteinander verknüpfen, um den Variationskoeffizient (CV) zu berechnen:

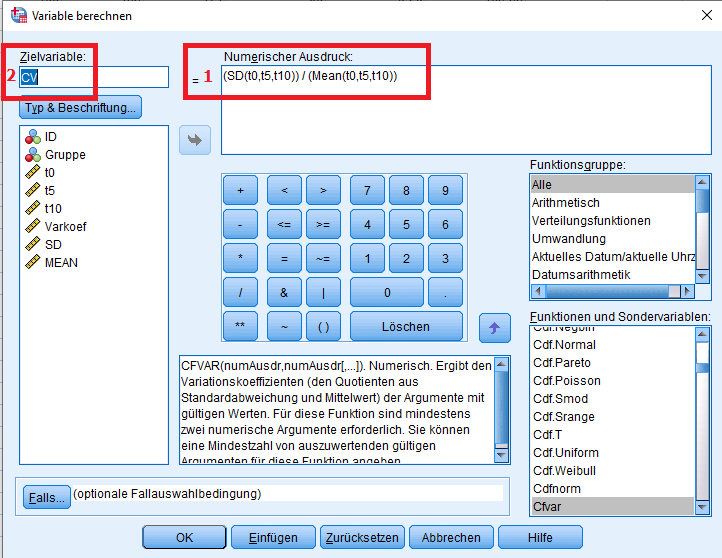
Entsprechend sind alle Werte der Messreihe je Proband auszuwählen (hier: t0, t5 und t10). Man kann auch mit Zwischenschritten zunächst den Mittelwert und die Standardabweichung als neue Variablen berechnen und dann den Variationskoeffizienten (= coefficient of variation = CV) nach obiger Formel berechnen.

Das Ergebnis (CV) ist logischerweise identisch mit der hinterlegten Funktion, die ich oben mit Varkoef verwendet habe:

 

2 Variationskoeffizient für das long-Format in SPSS berechnen

Im Gegensatz zum wide-Format gibt es in SPSS keine Formel für das sog. long-Format. Hier hilft nur, mit dem Wissen um die Berechnung des Variationskoeffizienten die Bestandteile durch SPSS ausgeben und diese dann im nächsten Schritt manuell miteinander in Form eines Quotienten zu verknüpfen.

   

Für dieses Beispiel möchte ich den Variationskoeffizienten für Größe (in m) und Gewicht (in kg) berechnen.

 

Laut obiger Formel brauche ich hierfür lediglich Mittelwert und Standardabweichung für beide Variablen.

Dies geht über Analysieren -> Deskriptive Statistiken -> Deskriptive Statistik…

 

Als Nächstes sind lediglich die Variablen von Interesse, für die der Variationskoeffizient berechnet werden soll. In meinem Falle also Größe und Gewicht:

 

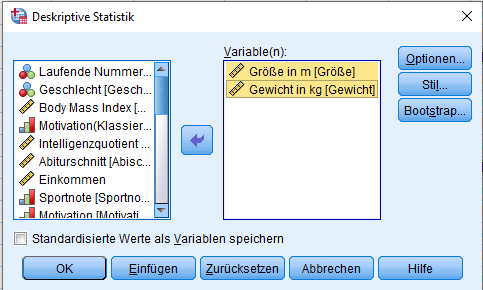
Mit einem Klick auf OK wird dies nun von SPSS berechnet.

Es ist erkennbar, dass die Wertebereich sich deutlich unterscheiden, demzufolge auch die davon abhängige Standardabweichung. Sie ist beim Gewicht grob gesagt 100-mal höher als bei der Größe.

Nun kann die einfache Berechnung des Variationskoeffizienten vorgenommen werden.

   

bzw.

   

Es ist erkennbar, dass der vermeintlich große Unterschied in der Streuung v.a. auf den Wertebereich der Variablen zurückzuführen ist. Wenn hierfür mit einem relativen Streumaß wie dem Variationskoeffizient kontrolliert wird, ist die Streuung beim Gewicht nur in etwa 3-mal höher als bei der Größe.

 

3 Videotutorial

Fragen können unter dem verlinkten Video gerne auf YouTube gestellt werden.