Inhaltsverzeichnis
1 Ziel des t-Test bei unabhängigen Stichproben in Excel
Der t-Test für unabhängige Stichproben in Excel testet, ob bei zwei unabhängigen Stichproben die Mittelwerte unterschiedlich sind. Für abhängige Stichproben ist der t-Test für verbundene Stichproben zu rechnen. In SPSS gibt es den t-Test für unabhängige Stichproben auch.
2 Voraussetzungen des t-Test bei unabhängigen Stichproben in Excel
Die wichtigsten Voraussetzungen sind:
- zwei voneinander unabhängige Stichproben/Gruppen
- metrisch skalierte y-Variable
- normalverteilte Fehlerterme innerhalb der Gruppen
- Bei unterschiedlichen Gruppengrößen: Homogene (nahezu gleiche) Varianzen der y-Variablen über die Gruppen – per Augentest, notfalls über z.B. Levene-Test
- Achtung: Mindeststichprobengröße bedenken – über eine Poweranalyse zu ermitteln
3 Durchführung des t-Test bei unabhängigen Stichproben in Excel
“Trainierte Personen haben einen niedrigeren Ruhepuls als untrainierte Personen.”
Über das Menü in Excel: Reiter “Daten” > “Datenanalyse” > “Zweistichproben t-Test: Gleicher Varianzen”.
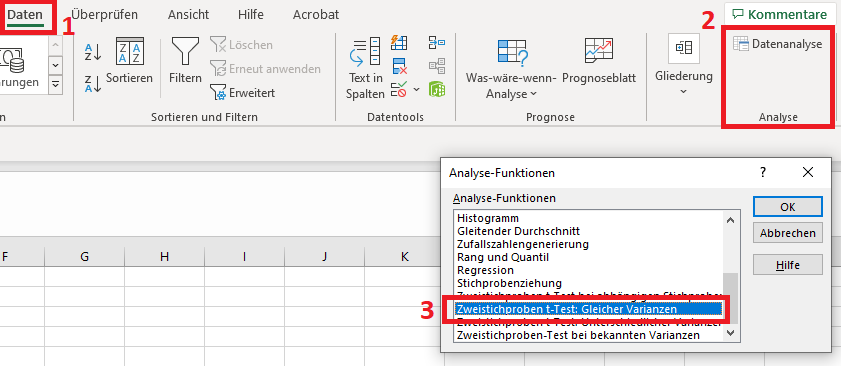
Hinweis: Sollte die Funktion “Datenanalyse” nicht vorhanden sein, ist diese über “Datei” > “Optionen” > “Add-Ins” > “Verwalten” -> “Los…” zu aktivieren. Dieses Video zeigt dies kurz.
Als Bereich Variable A markiert man die beobachteten Werte der ersten Stichprobe. Im Bereich Variable B sind es entsprechend die beobachteten Werte der zweiten Stichprobe. Unten ist zu sehen, dass B3-B15 die eine Variable bzw. Gruppe und E3-E15 die andere Gruppe bzw. Variable ist.
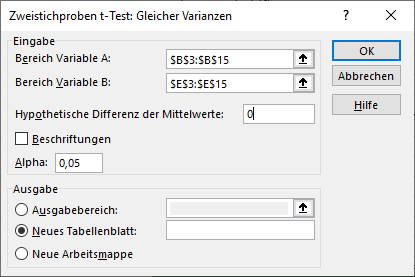
Bei “Hypothetische Differenz der Mittelwerte” ist eine “0” einzutragen Dies hat zur Folge, dass Excel folgende Nullhypothese testet: die beiden Stichproben stammen aus der gleichen Grundgesamtheit und besitzen damit ähnliche (“gleiche”) Mittelwerte.
Sollte in den Bereichen A und B eine Beschriftung mit markiert worden sein, ist bei “Beschriftungen” ein Haken zu setzen. Dadurch wird die erste Zeile, die dann die Beschriftung enthält, ignoriert.
Als Alpha ist das Alphafehler-Niveau einzutragen. Hier ist typischerweise 5% also 0,05 zu wählen. Es besteht auch die Möglichkeit eine geringere Wahrscheinlichkeit für einen Fehler 1. Art zu wählen. Das entspricht einer geringeren Wahrscheinlichkeit, die Nullhypothese fälschlicherweise abzulehnen, also einen Effekt zu unterstellen, der nicht vorhanden ist..
4 Interpretation des t-Test bei unabhängigen Stichproben in Excel
4.1 Die Voraussetzung der Varianzhomogenität
Pauschal empfehle ich folgendes Vorgehen:
- Zunächst ist Varianzhomogenität nur dann relevant, wenn die Gruppengrößen ungleich sind (vgl. Field (2018), S. 259). In meinem Fall sind sie mit jeweils 13 Beobachtungen sogar exakt gleich groß, weshalb Varianzhomogenität keine Rolle spielt – die Varianzen sind aber ohnehin sehr ähnlich (siehe unten).
- Sollten die Gruppengrößen ungleich sein (Daumenregel ab +/- 15%), genügt ein Augentest. Weichen die Varianzen maximal 20% voneinander ab, stellt dies i.d.R. kein Problem dar.
- Der Levene’s Test ist die analytische Methode zur Testung. Er ist allerdings bei großen Stichroben zu sensitiv bei unbedeutenden Abweichungen und bei kleinen Stichproben nicht sensitiv genug (vgl. Field (2018), S. 259). Sollte er dennoch berichtet werden müssen, zeige ich die Durchführung in diesem Blogbeitrag sowie Video.
- Sind die Varianzen nicht homogen bzw. gleich, muss ein t-Test mit unterschiedlichen Varianzen gerechnet werden. Die Auswahl ist im Menü analog zu oben:
Reiter “Daten” > “Datenanalyse” > “Zweistichproben t-Test: Unterschiedlicher Varianzen”.
Möchte man stets auf Nummer sicher gehen, wird pauschal der t-Test bei ungleichen Varianzen gerechnet: Die Auswahl und Berechnung ist analog zu oben möglich: Reiter “Daten” > “Datenanalyse” > “Zweistichproben t-Test: Unterschiedlicher Varianzen”.
Logik hinter der pauschalen Rechnung: Liegen Verletzungen vor, wird für diese korrigiert. Liegen keine Verletzungen vor, erfolgt keine Korrektur (vgl. Field (2018), S.259).
4.2 Signifikanz des Tests
Neben den standardmäßig ausgegebenen Mittelwert, Varianzen, Beobachtungen usw. ist das Augenmerk auf den p-Wert (“P(T<=t) einseitig” bzw. “P(T<=t) zweiseitig”) zu richten.
Ausgabe des Zweistichproben t-Test unter der Annahme gleicher Varianzen
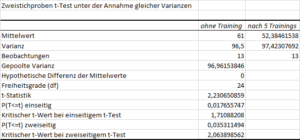
ACHTUNG: Hat man bereits eine Vermutung, dass z.B. eine Gruppe einen höheren/niedrigeren Wert hat, ist dies eine gerichtete Hypothese (siehe blaue Box, Abschnitt 3) und man muss 1-seitig testen – sofern die Mittelwerte Anlass dazu geben und die Vermutung widerspiegeln. Dies ist in meinem Fall gegeben, da der Mittelwert der Trainierten mit 52,38 kleiner ist als der Untrainierten mit 61. Demzufolge interessiert nur der Wert hinter “P(T<=t) einseitig”.
Ist der p-Wert (hier: p = 0,018) hinreichend klein bzw. kleiner als Alpha (z.B. 0,05), geht man davon aus, dass die Gruppen nicht aus derselben Grundgesamtheit stammen.
Oder anders formuliert: man kann von nicht zufälligen Unterschieden hinsichtlich der Mittelwerte zwischen den Gruppen ausgehen.
Alternativ kann man statt dem p-Wert auch die sog. “t-Statistik” (hier 2,231) zur Beurteilung heranziehen. Sie ist in Verbindung mit den Freiheitsgraden (24) mit dem “Kritischen t-Wert bei einseitigem t-Test” bzw. “Kritischen t-Wert bei zweiseitigem t-Test” zu vergleichen. Ist der kritische t-Wert (errechnet 1,71) kleiner als die t-Statistik, ist die Nullhypothese von Gleichheit ebenfalls zu verwerfen. Ob einseitig oder zweiseitig zu testen ist, ist analog zu 3. zu entscheiden.
4.3 Effektstärke des Tests
Nachdem festgestellt wurde, dass Unterschiede zwischen den Gruppen existieren, ist die Größe dieses Unterschiedes zu quantifizieren.
Nicht vergessen: Der p-Wert sagt nichts über die Stärke des Unterschiedes. Er beschreibt lediglich die Wahrscheinlichkeit, dass der beobachtbare Unterschied zufällig zustande gekommen ist.
4.3.1 Cohen’s d manuell berechnen
![\[ d = \frac{\bar{x_{1}}-\bar{x_{2}}}{s}} \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-5e88e7c39a31e9520d17fe93def179fd_l3.png "Rendered by QuickLaTeX.com")
![\[s = \sqrt{\frac{(n_{1}-1)\cdot s_{1}^{2} + (n_{2}-1)\cdot s_{2}^{2}} {n_{1}+n_{2}-2}} \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-caf462eff0873927a026ce8f5d42c09f_l3.png "Rendered by QuickLaTeX.com")
![\[s = \sqrt{\frac{s_{1}^{2}- s_{2}^{2}}{2}} \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-9f97fe989bd4b4ccefbd3d7b76d01a85_l3.png "Rendered by QuickLaTeX.com")
Im Beispiel sind die Mittelwerte 61 und 52,38 (siehe oben) sowie die gepoolte Standardabweichung 9,85. Eingesetzt in die obige Formel:
![\[ d = \frac{61-52,38}{9,85}} = 0,875 \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-e5b3ce93625f5e97b666e2e0f1f2b316_l3.png "Rendered by QuickLaTeX.com")
Diese Größe wird mit Hilfe vergleichbarer Studien eingeordnet. Behelfsweise werden fachspezifische Grenzen verwendet.
Ist beides nicht vorhanden, kann Cohen (1988/1992) herangezogen werden:
- ab d = 0,2 klein,
- ab d = 0,5 mittel und
- ab d = 0,8 stark.
Im Beispiel liegt der Wert 0,875 über der Grenze zum starken Effekt. Somit ist der Unterschied zwischen den beiden Gruppen bzw. deren Ruhepulsen stark.
4.3.2 Effektstärkemaß r manuell berechnen
Eine zweite Möglichkeit ist die manuelle Berechnung von r sowie die Beurteilung anhand Cohen: Statistical Power Analysis for the Behavioral Sciences (1988), S. 79-81. Cohen selbst merkt aber an, dass die Effektstärkemaße und deren Klassengrenzen nicht 1:1 vergleichbar sind. Vorzuziehen ist Cohen’s d. Die Berechnung von r erfolgt über die Formel mit t² als quadrierter T-Wert und df als degrees of freedom (Freiheitsgrade).
![\[ r = \sqrt{\frac{t^2}{t^2+df}} \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-ea814ae95eca7b794de9e0f93fef19d1_l3.png "Rendered by QuickLaTeX.com")
Ab 0,1 ist es ein schwacher Effekt, ab 0,3 ein mittlerer und ab 0,5 ein starker Effekt.
Im Beispiel ist der t-Wert 2,231 und die Freiheitsgrade (df) 24. Eingesetzt in die Formel:
![\[ r = \sqrt{\frac{2,231^2}{2,231^2+24}}= 0,414 \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-17f504add46caafc8eeda1a987f240c9_l3.png "Rendered by QuickLaTeX.com")
Das Ergebnis von 0,414 liegt über der Grenze zur mittleren Effektstärke und der Unterschied ist damit laut Cohen ein mittelstarker Unterschied. Allerdings gibt es neuere Richtlinien bzgl. r, die von Gignac, Szodorai (2016) vorgeschlagen wurden, die bei 0,1 (klein), 0,2 (mittel) und 0,3 (groß) liegen. Demnach wäre der Unterschied im Beispiel ein großer.
5 Videotutorials
6 Reporting des t-Tests bei unabhängigen Stichproben
Gruppenmittelwerte und Standardabweichungen sind zu berichten. Zusätzlich die t-Statistik mit Freiheitsgraden, der p-Wert (je nach Hypothese ein- oder zweiseitig) und die Effektstärke (vorzugsweise Cohen’s d):
t(df) = t-Wert; p-Wert; Effektstärke d.
Bei untrainierten Personen (M = 61; SD = 9,82) ist im Vergleich mit trainierten Personen (M = 52,38; SD = 9,87) ein höherer Ruhepuls beobachtbar, t(24) = 2,23; p = 0,035; d = 0,88. Nach Cohen (1992) ist dieser Unterschied groß.
7 Literatur
- Cohen, J. (1988). Statistical power analysis for the behavioral sciences. New York, NY: Psychology Press, Taylor & Francis Group
- Cohen, J. (1992). A power primer. Psychological bulletin, 112(1), 155-159.
- Field, A. (2018), Discovering Statistics Using IBM SPSS Statistics, SAGE.
- Gignac, G. E., & Szodorai, E. T. (2016). Effect size guidelines for individual differences researchers. Personality and individual differences, 102, 74-78.
Weitere nützliche Tutorials findest du auf meinem YouTube-Kanal.
