Im Vorfeld jeder statistischen Untersuchung sollte mittels einer Poweranalyse sichergestellt werden, dass eine hinreichend große Menge an Probanden/Beobachtungen vorliegt. Warum? Kurz gesagt, damit der Test auch die Chance hat, einen Effekt erkennen zu können. Diese Chance nennt man auch statistische Power.
Inhaltsverzeichnis
1 Vorbemerkungen
1.1 Statistische Power (Teststärke)
Teststärke (sog. statistische Power) beschreibt die Fähigkeit eines Tests, einen in der Stichprobe tatsächlich vorhandenen Effekt auch erkennen zu können und ist essenziell – nur leider ist das zu wenig bekannt. Beim verbundenen t-Test ist der Effekt offensichtlich ein Unterschied einer Population vor und nach einer Intervention, also zu zwei Messzeitpunkten.
Die Power berechnet sich aus 1 abzüglich des Beta-Fehlers.
Der Beta-Fehler beschreibt das fälschliche Beibehalten der Nullhypothese. Hier kann man gut erkennen, dass Power und Beta-Fehler (auch Fehler 2. Art) direkt zusammenhängen. Ich erhöhe die Power, wenn ich den Beta-Fehler minimiere. Hier sind 5% Fehlerwahrscheinlichkeit erstrebenswert, somit ist die Power 1 – 0,05 = 0,95 (95%). Mehr ist kaum praktikabel. Als Kompromiss findet man als Untergrenze 0,8 – also 80%. Eine geringere Power im Vorfeld anzunehmen, ist kaum rechtfertigbar. Auch 0,8 muss begründet sein.
1.2 Alpha-Fehler
Der Alpha-Fehler (auch Fehler 1. Art) ist das fälschliche Ablehnen der Nullhypothese. Typisch ist als Grenze für Alpha 5% (0,05). Man akzeptiert also eine maximale Alpha-Fehlerwahrscheinlichkeit von 5%. Weitere typische Grenzen sind 1%, 0,1% oder sogar 10%. Achtung, es kommt hier häufig auf den Kontext an. Niedriger kann pauschal als besser erachtet werden – es geht ja um die Fehlervermeidung.
1.3 Effektstärke
Im Vorfeld benötigt man die Effektstärke, also wie stark der beobachtete Effekt wohl sein wird bzw. vermutet wird. Im Kontext des t-Tests bei verbundenen Stichproben verwendet man Cohens d nach Cohen (1988)/Cohen (1992). In G*Power wird allerdings nicht d, sondern dz verwendet. Vereinfacht ausgedrückt wird aus den Werten der Messzeitpunkten eine Differenz gebildet. Für diese Differenz ergeben sich Mittelwert und Standardabweichung, aus denen lediglich der Quotient gebildet wird, also die Abweichung standardisiert:
![\[ d_{z}=\frac{M_{diff}}{SD_{difff}} \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-14d1f84b7c4176868424e68ef462d790_l3.png "Rendered by QuickLaTeX.com")
Es gibt hierzu verschiedene Herangehensweisen zur Festlegung im Rahmen der Poweranalyse:
- Der einfachste Weg ist eine Orientierung an Vergleichsstudien und Verwendung der dort angegebenen Effektstärke dz. Sollte keine angegeben sein, kann man die mitunter nachträglich mit den angegebenen Populationsparametern nach obiger Formel ermitteln.
- Der praktische Weg ist das Festlegen auf Basis der Erfahrung des Forschers. Dies ist aber subjektiv und eine Begründung mit persönlicher Erfahrung kann bei Gutachtern schnell zu einer ablehnenden Haltung führen.
- Der pragmatische Weg ist die Annahme eines mittleren Effektes (dz = 0.5). Auch hier ist eine Begründung notwendig und kann nicht einfach so getroffen werden – nicht selten findet man aber keine.
Die Konventionen nach Cohen sind folgende:
- d > 0,2 – kleiner Effekt
- d > 0,5 – mittlerer Effekt
- d > 0,8 – großer Effekt
1.4 Gerichtetheit der Hypothese
Naiv testet man ungerichtet, also zweiseitig. Man weiß also nicht, ob sich der Messwert nach der Intervention positiv oder negativ entwickelt. (Werte unterscheiden zwischen Zeitpunkten). Testet man einseitig, vermutet man im Vorfeld, dass zum Zeitpunkt 2 die Testvariable höher (oder niedriger) als zum Zeitpunkt 1 ist.
2 Die Mindeststichprobengröße mit G*Power
Zunächst ist der richtige Test auszuwählen, was am einfachsten über das obere Menü funktioniert.
Means -> Two Dependent Groups (matched pairs)
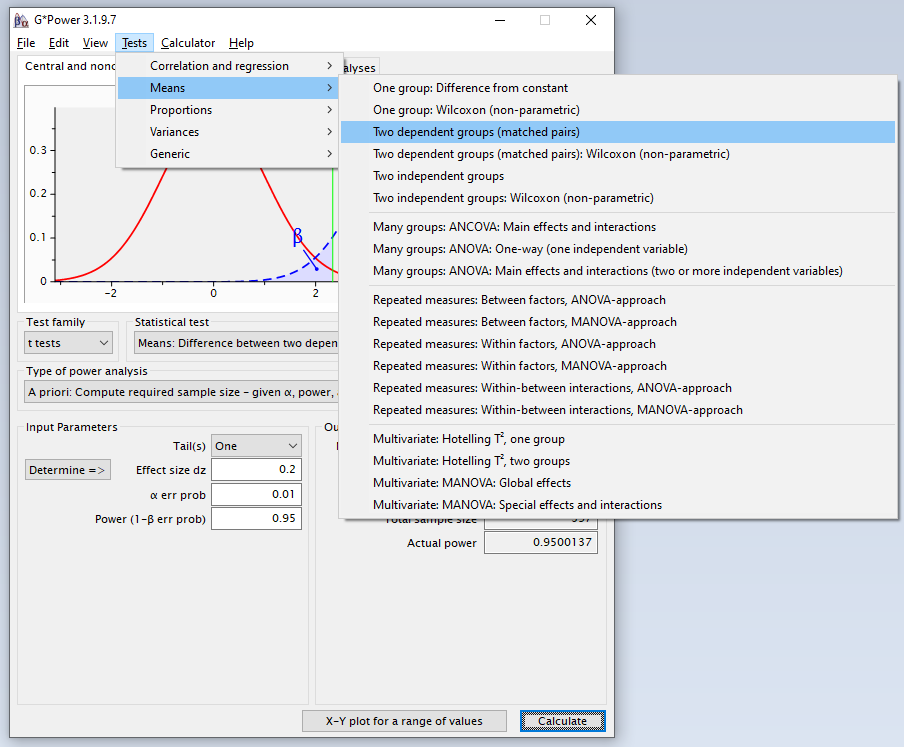
Bei Type of Power Analysis ist zwingend a priori auszuwählen.
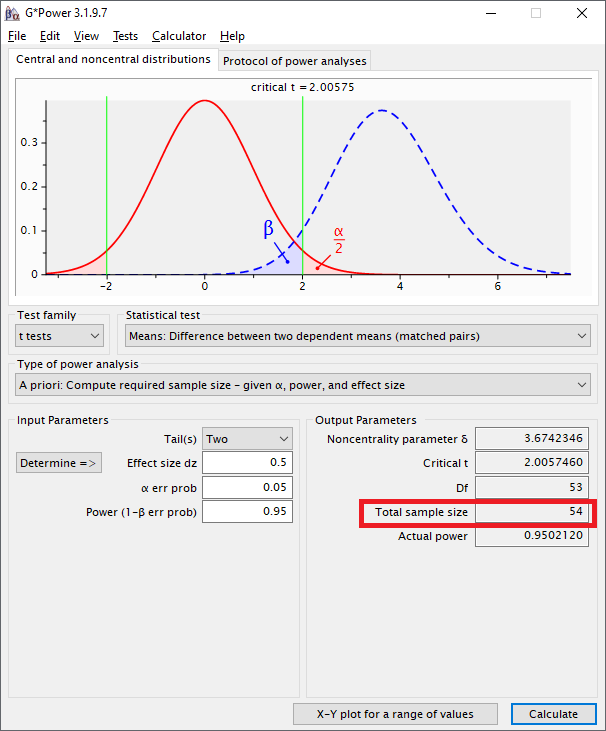
Entsprechend sind nun Gerichtetheit des Tests, Effektstärke (vermutetes Cohens d, siehe oben), Alphafehler (typisch 5%) sowie statistische Power (typisch 95%) einzutragen.
Bei einem zweiseitigen Test mit mittlerer Effektstärke von dz = 0,5, Alpha 5% und einer Power von 95% ergibt dies einen mindestens notwendigen Stichprobenumfang von n = 54 Beobachtungen. Es sind also 54 Beobachtungen zu jeweils zwei Zeitpunkten notwendig.
3 Powertabellen
3.1 Zweiseitiges Testen
Hier eine Übersicht für verschiedene Effektstärken bei unterschiedlichen Power-Niveaus bei zweiseitigem Test:
Zweistichproben t-Test (2-seitig)
Cohens d Alpha Power (1-Beta) N
0,8 0,05 0,95 23
0,5 0,05 0,95 54
0,2 0,05 0,95 327
0,8 0,05 0,8 15
0,5 0,05 0,8 34
0,2 0,05 0,8 199
0,2 0,01 0,95 449
Es ist recht deutlich erkennbar, dass mit sinkender Effektstärke bei gleichbleibender Power die notwendige Stichprobengröße (N) stark steigt. Der “worst case” wäre eine kleine Effektstärke von 0,2 bei einem Alphafehler von 1% sowie einer Power von 95%. Hier wären insgesamt 449 Beobachtungen zu zwei Zeitpunkten notwendig.
3.2 Einseitiges Testen
Die Übersicht für verschiedene Effektstärken bei unterschiedlichen Power-Niveaus bei einseitigem Test:
Zweistichproben t-Test (1-seitig)
Cohens d Alpha Power (1-Beta) N
0,8 0,05 0,95 19
0,5 0,05 0,95 45
0,2 0,05 0,95 272
0,8 0,05 0,8 12
0,5 0,05 0,8 27
0,2 0,05 0,8 156
0,2 0,01 0,95 397
Man kann hier gut erkennen, dass bei einseitigen Tests ein wenig an der Mindeststichprobengröße “gespart” werden kann. Es hilft also im Vorfeld gerichtete Hypothesen aufzustellen.
4 Videotutorial
5 Literatur
- Cohen, J. (1988). Statistical power analysis for the behavioral sciences. New York, NY: Psychology Press, Taylor & Francis Group
- Cohen, J. (1992). A power primer. Psychological bulletin, 112(1), 155-159.
