Inhaltsverzeichnis
1 Ziel des Spearman-Korrelationskoeffizienten in SPSS
Der Korrelationskoeffizient nach Spearman hat das Ziel, einen ungerichteten Zusammenhang zwischen zwei ordinalen Variablen zu untersuchen. Er zeigt entweder einen positiven Zusammenhang, einen negativen Zusammenhang oder keinen Zusammenhang. In der Nullhypothese geht er von keinem Zusammenhang aus.
2 Voraussetzungen des Spearman-Korrelationskoeffizienten in SPSS
- zwei ordinal skalierte Variablen oder eine metrisch skalierte und eine ordinal skalierte Variable
- Häufig genannt: Linearität – gerade das untersucht man mit der Korrelation nach Spearman aber ohnehin
Sind die Voraussetzungen nicht erfüllt und ihr wollt dennoch korrelieren, schaut im Beitrag zur richtigen Wahl des Korrelationskoeffizienten nach Alternativen.
3 Voraussetzungsprüfung für den Spearman-Korrelationskoeffizienten
Ordinale Variablen sind daran zu erkennen, dass sie in SPSS das ein kleines Histogramm bzw. Säulendiagramm als Messniveau besitzen. Wenn man nicht sicher ist, ob tatsächlich ein ordinales Messniveau der Variable vorliegt, sollte man prüfen, ob es eine aufsteigende oder absteigende Reihenfolge der Ausprägungen der Variable gibt. Variablen wie Zustimmung zu einer Aussage oder Zufriedenheit mit einem Produkt oder Einkommensklassen erfüllen dieses Kriterium. Fasst man allerdings mehrere solche Variablen (z.B. via Mittelwert) zusammen, bildet also einen Score, werden sie häufig als als quasi-metrisch eingestuft, was eine Korrelation nach Pearson ermöglicht.
4 Durchführung der Korrelation nach Spearman in SPSS
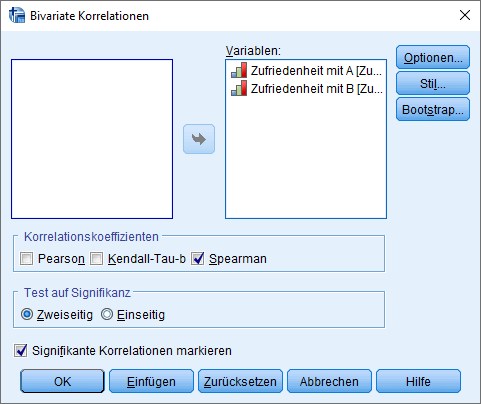
Die Korrelation nach Spearman ist aufzurufen über Analyse -> Korrelation -> Bivariat. Die zu korrelienderen Variablen sind in das Feld Variablen zu übertragen. Unter Korrelationskoeffizienten stehen Pearson, Kendall-Tau-b und Spearman zur Wahl. Entsprechend ist hier Spearman auszuwählen. Im Beispiel korreliere ich zwei Variablen zu Produktzufriedenheiten (“Zufriedenheit mit A” und “Zufriedenheit mit B”). Weitere Einstellungen werden von mir nicht vorgenommen und ich starte die Berechnung mit OK. Hinweis: Es kann natürlich eine Vielzahl von Variablen miteinander korreliert werden. Meist macht man das im Rahmen der Multikollinearitätsprüfung.
Pauschal Variablen jeglicher Skalenniveaus miteinander zu korrelieren – z.B. im Rahmen einer Regression – ist allerdings nicht nötig. Im Gegenteil, Korrelation ist keine notwendige Voraussetzung für Kausalität. Unter dem Begriff der Scheinkausalität bzw. “Cum hoc ergo propter hoc” wird dies in der Wissenschaft beschrieben.
5 Interpretation der Ergebnisse der Korrelation nach Spearman in SPSS
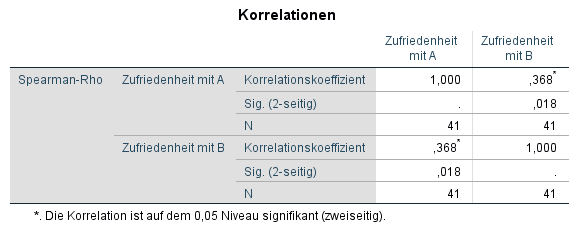
Die zu interpretierenden Ergebnistabelle ist aufgrund nur zweier korrelierter Variablen recht übersichtlich. Generell gilt, dass diese Tabelle stets alle Variablen in den Zeilen und Spalten aufführt und somit auch symmetrisch aufgebaut ist. Dass Zufriedenheit mit A und Zufriedenheit mit B jeweils mit sich selbst perfekt korrelieren (r =1), dürfte klar sein und bedarf keiner Interpretation. Vielmehr interessiert in dieser Tabelle der Wert rechts oben oder links unten. Dieser beschreibt die Korrelation nach Spearman von “Zufriedenheit mit A” und “Zufriedenheit mit B” und hat einen Wert von r = 0,368.
Er ist zudem statistisch signifikant. SPSS gibt eine Signifikanz von p = 0,018 an, was unter dem typischen Alphaniveau von 0,05 liegt. Hat man eine Signifikanz von unter 0,05, verwirft man die Nullhypothese, dass kein Zusammenhang bzw. keine Korrelation zwischen den Variablen besteht. Hier ist dies wie gesagt der Fall. Die Variablen korrelieren miteinander.
Da r >0, geht man hier von einer positiven Korrelation, also einem positiven Zusammenhang von der “Zufriedenheit mit A” und “Zufriedenheit mit B” aus. Das könnte auch nachvollziehbar sein. Ist man mit dem einen Produkt zufrieden, trifft dies auch auf ein anderes Produkt zu. Denkbar wären Müslisorten eines Herstellers oder Kaffeesorten aus einer bestimmten Anbauregion. Mag ich das eine, mag ich das andere auch eher und umgekehrt: gefällt mir das eine nicht, gefällt mir auch das andere eher nicht. Eine negative Korrelation würde bedeuten, dass mir das eine Produkt gefällt, gleichzeitig das andere aber wiederum nicht.
Zusammenfassend kann mittels der Spearman-Korrelation hier ein statistisch signifikanter positiver Zusammenhang zwischen “Zufriedenheit mit A” und “Zufriedenheit mit B” beobachtet werden.
6 Ermittlung der Effektstärke des Spearman-Korrelationskoeffizienten
Die Effektstärke ist im Rahmen der Korrelation der Korrelationskoeffizient r selbst. Laut Cohen: Statistical Power Analysis for the Behavioral Sciences (1988), S. 79-81 sind die Effektgrenzen 0,1-0,3 (schwach), 0,3-0,5 (mittel) und größer 0,5 (stark).
Im vorliegenden Beispiel ist die Effektstärke mit 0,368 > 0,3 und damit gerade noch mittel. Es handelt sich also um eine mittlere Korrelation zwischen “Zufriedenheit mit A” und “Zufriedenheit mit B”.
Weitere nützliche Tutorials findest du auf meinem YouTube-Kanal.


