Inhaltsverzeichnis
1 Ziel des Pearson-Korrelationskoeffizienten in R
Der Pearson-Korrelationskoeffizient bzw. Bravais-Pearson-Korrelationskoeffizient hat das Ziel einen ungerichteten Zusammenhang zwischen zwei metrischen Variablen zu untersuchen. Er zeigt entweder einen positiven Zusammenhang, einen negativen Zusammenhang oder gar keinen Zusammenhang zwischen den Variablen.
Nullhypothese: es existiert kein Zusammenhang zwischen den beiden Variablen.Soll für weitere Einflussfaktoren kontrolliert werden, kann eine Partialkorrelation gerechnet werden.
2 Voraussetzungen des Pearson-Korrelationskoeffizienten in R
- zwei metrisch skalierte Variablen, im Zweifel kann auch eine Korrelation nach Spearman oder Kendall-Tau gerechnet werden.
- bivariate bzw. univariate Normalverteilung – siehe unten
- Häufig genannt: Linearität – gerade das untersucht man mit der Pearson-Korrelation aber ohnehin.
Sind die Voraussetzungen nicht erfüllt und ihr wollte dennoch korrelieren, schaut im Beitrag zur richtigen Wahl des Korrelationskoeffizienten nach Alternativen.
3 Voraussetzungsprüfung für den Pearson-Korrelationskoeffizienten
3.1 Metrische Variablen
Metrische Variablen sind daran zu erkennen, dass die Abstände zwischen den Ausprägungen gleich sind und diese auch als solche interpretiert werden können (Ausführlicher Artikel zu den Messniveaus). Variablen wie Größe, Gewicht, € usw. erfüllen dieses Kriterium. Es ist häufig auch zulässig, Skalen, die aus mehreren Items zusammengesetzt sind (z.B. via Mittelwert), als quasi-metrisch einzustufen. Eine Korrelation nach Pearson kann in solchen Fällen auch gerechnet werden. Bei größeren Stichproben ist aber auch diese Voraussetzung vernachlässigbar.
3.2 Bivariate Normalverteilung
Bivariate Normalverteilung (auch zweidimensionale Normalverteilung) beschreibt eine Normalverteilung der einen Variable für jeden Wert der anderen Variable. In R kann diese mittels des MVN-Pakets geprüft werden. Behelfsweise kann man univariate Normalverteilungen der beiden Variablen prüfen. Hierzu ist es genügend, über die hist()-Funktion ein Histogramm je Variable zu erzeugen und zu beurteilen. Erkennt man hier in etwa Normalverteilung, kann man mit der eigentlichen Korrelation nach Pearson fortfahren.
4 Grafische Darstellung des Zusammenhanges in R
Parallel zu jeder Korrelation nach Pearson kann eine kleine Visualisierung des Zusammenhanges mittels Streudiagramm erfolgen. Das funktioniert mit dem plot()-Befehl: Für weitere grafische Anpassungen gibt es diesen Beitrag. Ich stelle hier den Zusammenhang zwischen Gewicht und Größe dar.
plot(df$Gewicht, df$Größe)
Im Ergebnis erhält man folgendes Diagramm:
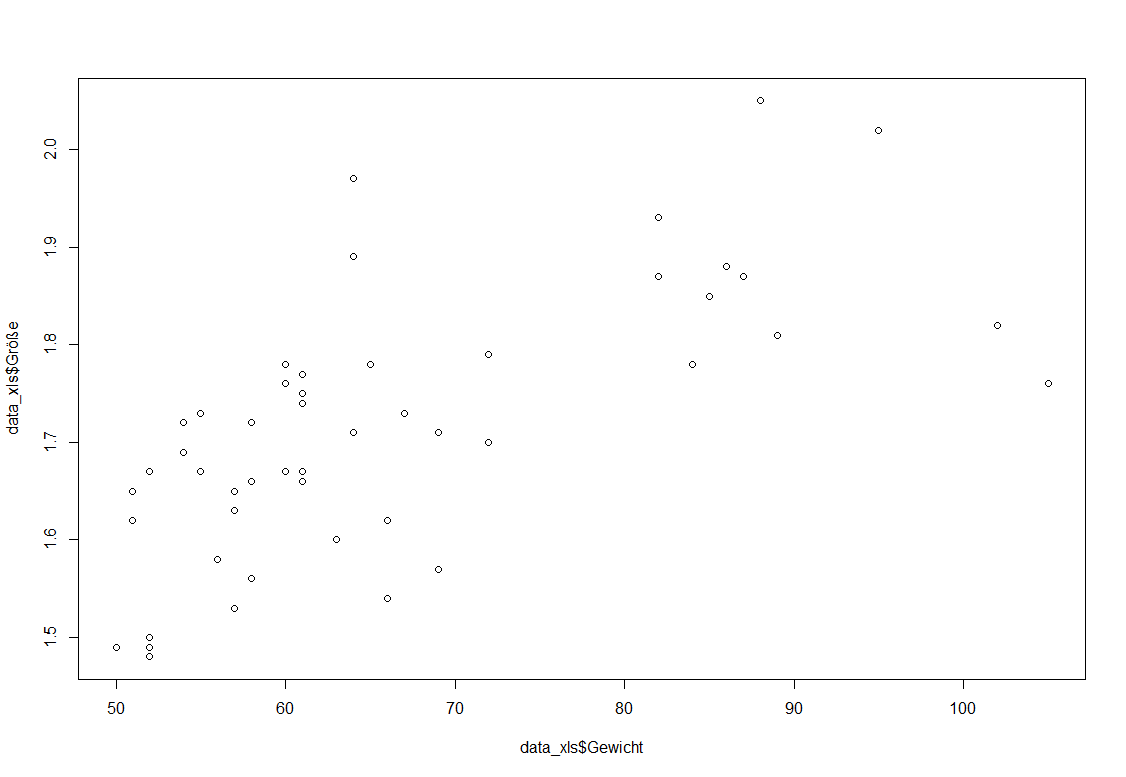
Erkennbar ist: mit zunehmendem Gewicht nimmt auch die Größe zu bzw. umgekehrt. Ein positiver Zusammenhang ist also naheliegend. Wie stark ist dieser allerdings? Dazu berechnet man den Pearson-Korrelationskoeffizient.
5 Berechnung der Korrelation nach Pearson in R
Die Korrelation nach Pearson ist zunächst denkbar einfach über die cor()-Funktion. Ich korreliere Gewicht und Größe miteinander, indem ich sie lediglich per Komma getrennt in die cor()-Funktion einfüge. Da ich den Dataframe nicht mit der attach-Funktion angehängt habe, verwende ich jeweils “df$” für die Variable. Ein weiteres Argument braucht es innerhalb der cor()-Funktion nicht.
cor(df$Gewicht, df$Größe)
[1] 0.6692971
Zwar wird mit 0,669 die Korrelation ausgegeben, die Signifikanz (p-Wert) fehlt jedoch, um die o.g. Nullhypothese verwerfen zu können oder nicht. Im Rahmen der cor.test()-Funktion kann man, neben anderen Dingen, die Signifikant anfordern. Die Funktion ist analog zu cor() aufgebaut und benötigt lediglich die beiden zu korrelierenden Variablen mit Komma getrennt als Input:
cor.test(df$Gewicht, df$Größe)
6 Interpretation der Ergebnisse der Korrelation nach Pearson in R
Die cor.test()-Funktion produziert folgenden Ouput:
Pearson's product-moment correlation data:
df$Gewicht and df$Größe
t = 6.3057, df = 49, p-value = 7.895e-08
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval: 0.4827566 0.7977398
sample estimates: cor 0.6692971
Fett markiert sind die wesentlichen Ergebnisse.
- Der untere Wert (cor) ist der Korrelationskoeffizient nach Pearson, der logischerweise wie bei der cor()-Funktion r = 0,6692971 beträgt.
- Die Signifikanz steht etwas weiter oben und ist mit p = 7,895e-08 sehr klein. Genauer gesagt ist sie 0,00000007895.
- Sie ist also sehr sehr viel kleiner als die typische Verwerfungsgrenze von 0,05.
Die Nullhypothese keines Zusammenhanges kann demnach verworfen werden. - Die Alternativhypothese eines korrelativen Zusammenhanges zwischen Gewicht und Größe wird demnach angenommen.
Achtung: Eine Kausalität bedeutet das nicht. Es geht bei der Korrelation lediglich um das gleichzeitige Auftreten hoher und niedriger Ausprägungen beider Variablen.
7 Gerichtete Hypothese und einseitiges Testen
Wer die Signifikanz nicht händisch teilen möchte, kann natürlich auch in R das entsprechende Argument der cor.test()-Funktion hinzufügen. Das Argument heißt alternative und lässt den Nutzer die Alternativhypothese definieren. Es gibt die Möglichkeiten alternative=”greater” und alternative=”less”. Das kann verwirrend sein, denn “greater” steht für einen positiven Zusammenhang und “less” für einen negativen Zusammenhang. Am konkreten Beispiel unterstelle ich im Vorfeld einen positiven Zusammenhang:
cor.test(df$Gewicht, df$Größe, alternative="greater")
Das Ergebnis ist sehr ähnlich zu oben. Änderungen habe ich fett hervorgehoben:
df$Gewicht and df$Größe
t = 6.3057, df = 49, p-value = 3.948e-08
alternative hypothesis: true correlation is greater than 0
95 percent confidence interval: 0.5168666 1.0000000
sample estimates: cor 0.6692971
Die Pearson-Korrelation ist natürlich mit 0,6692971 unverändert. Allerdings sieht man, dass sich die Signifikanz von p = 7,895e-08 auf p = 3,948e-08 halbiert hat. Das ist Folge des einseitigen Testens. Zusätzlich ist die nun anzunehmende Alternativhypothese eindeutig formuliert. Korrelation ist größer 0 (“true correlation is greater than 0“) bedeutet, dass eine positive Korrelation vorliegt.
8 Ermittlung der Effektstärke des Pearson-Korrelationskoeffizienten
Die Effektstärke ist im Rahmen der Pearson-Korrelation der Korrelationskoeffizient r selbst.
Zunächst sollte ein Vergleich mit ähnlichen Studien vorgenommen werden. Sollten keine vergleichbaren Studien existieren, kann man fachspezifische Grenzen heranziehen.
Sollten auch diese nicht existieren, können die Grenzen von Cohen (1992), S. 157 herangezogen werden:- ab 0,1 (schwach),
- ab 0,3 (mittel) und
- ab 0,5 (stark).
Im vorliegenden Beispiel ist die Effektstärke mit 0,6692971 und beim Vergleich mit den Grenzen von Cohen (1992) > 0,5 und damit stark. Es handelt sich also um eine starke Korrelation zwischen Einkommen und Motivation.
Weitere nützliche Tutorials findest du auf meinem YouTube-Kanal.
9 Videotutorial
10 Literatur
Cohen, J. (1992). Quantitative methods in psychology: A power primer. Psychol. Bull., 112, 155-159.


