Inhaltsverzeichnis
1 Ziel des Tests der Residuen auf Normalverteilung
Grundsätzlich hat eine lineare Regression die Voraussetzungen, dass deren Residuen (nicht die unabhängigen oder die abhängige Variable an sich) in etwa normalverteilt sind. Prinzipiell gibt es dazu die grafische als auch die analytische Methode, die ich jeweils nachfolgend vorstellen werde.
2 Vorarbeiten für die Analyse
Zunächst bedarf es der Aufstellung eines linearen Modells, dessen Residuen letztlich auf Normalverteilung getestet werden sollen. Hierzu verwendet man die “lm()-Funktion”, mit der man das lineare Regressionsmodell definiert. In meinem Fall möchte ich den Abiturschnitt (mit Abischnitt abgekürzt) durch den Intelligenzquotient (IQ) erklären. Die Residuen sind einfach gesagt die Unterschiede zwischen den beobachteten, also den tatsächlichen y-Werten, und den durch das Modell geschätzten bzw. prognostizierten y-Werten.
model <- lm(Abischnitt~IQ, data = data_xls)
Im Rahmen der Berechnung des linearen Modells werden von R automatisch standardisierte und nicht standardisierte Residuen berechnet und im Modell-Summary gespeichert. Diese gilt es nun auf Normalverteilung zu prüfen. Man kann sie sich mit
rstandard(model)
bzw.
residuals(model)
ausgeben lassen, verwendet sie aber im Rahmen von Histogramm und Q-Q-Diagramm weiter.
3 Normalverteilung der Residuen in R testen: Grafische Methode
Es gibt insgesamt zwei Diagramme, die häufig zur Prüfung der Residuen auf Normalverteilung herangezogen werden und von R recht einfach ausgegeben werden können:
- Histogramm sowie
- Q-Q-Diagramm
3.1 Histogramm der Residuen erstellen und interpretieren
Das Histogramm bekommt man für die standardisierten bzw. nicht standardisierten Residuen mit dem Befehl “hist()”.
hist(rstandard(model))
hist(residuals(model))
Nachfolgend habe ich mir nur für die standardisierten Residuen ein Histogramm ausgeben lassen:
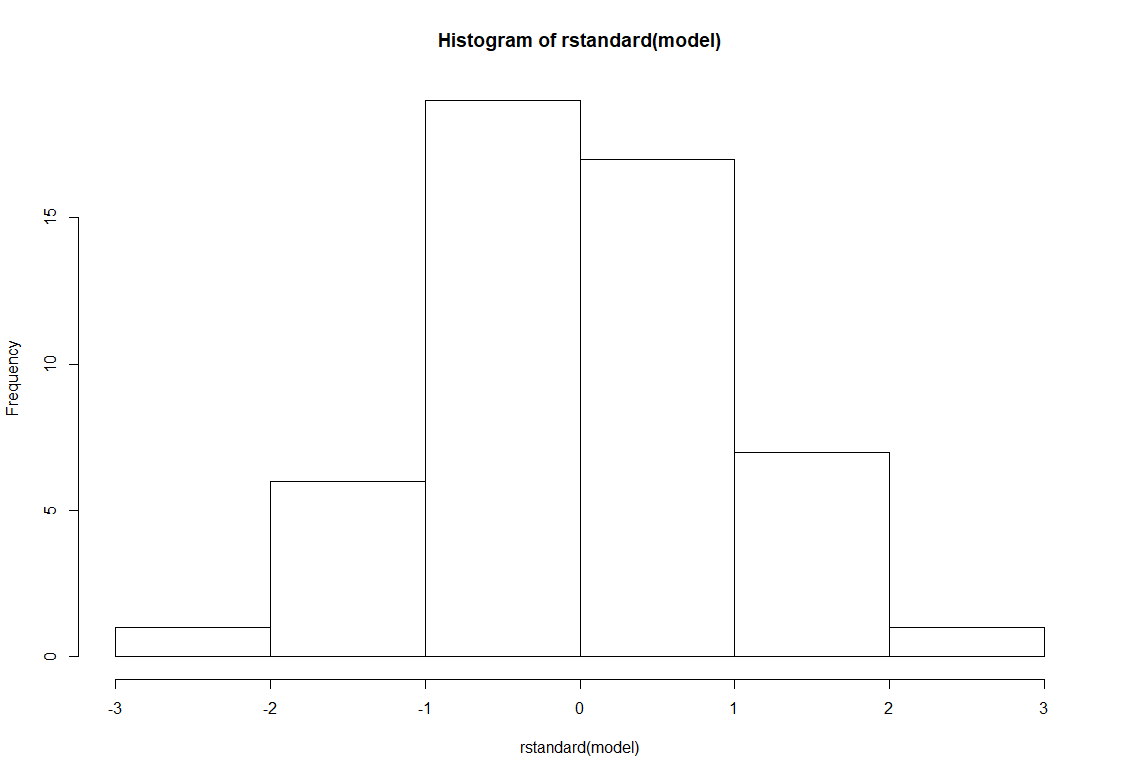
Die Interpretation ist hier recht einfach. Normalverteilung liegt in etwa vor, wenn in der Mitte des Histogramms mehr Residuen liegen als außen. Die oft zitierte Glockenform sollte erahnbar sein. Perfekte Normalverteilung sollte man nicht erwarten, weil es sie in praktischen Anwendungen kaum geben wird. Im Beispiel oben kann man schon eine sehr gute Normalverteilung erkennen. Hier würde man also von Normalverteilung der Residuen ausgehen und demzufolge die Voraussetzung als erfüllt ansehen.
3.2 Q-Q-Plot der Residuen erstellen und interpretieren
Das Q-Q-Diagramm erhält man mit dem qqnorm()-Befehl, in den man erneut rstandard(model) einsetzt:
qqnorm(rstandard(model))
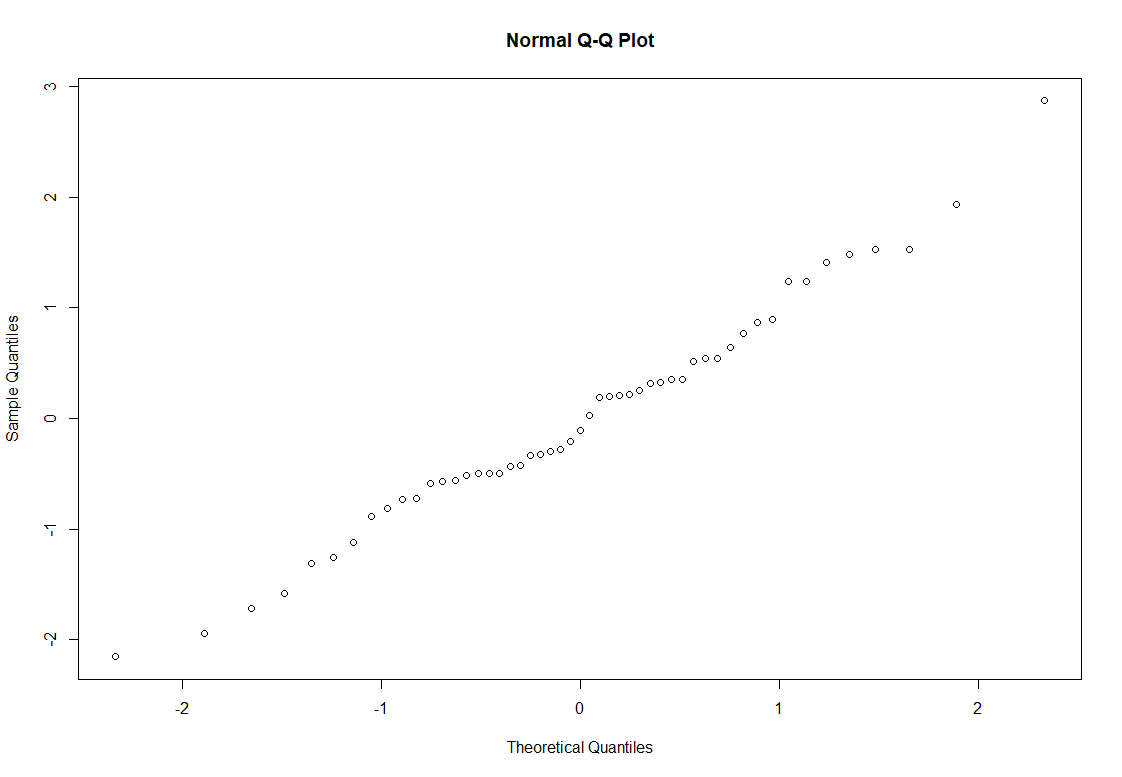
Auf den ersten Blick ist es hier nicht ganz so eindeutig. Perfekte Normalverteilung würde vorliegen, wenn man eine Ursprungsgerade erkennen würde. Eine Ursprungsgerade würde heißen, dass der x-Wert und der y-Wert identisch sind, also das theoretische Quantil dem Stichprobenquantil entsprechen würden. Um es etwas einfacher erkennen zu können, kann man sich eine Ursprungsgerade mit der Funktion qqline() zusätzlich einzeichnen zu lassen.
qqline(rstandard(model))
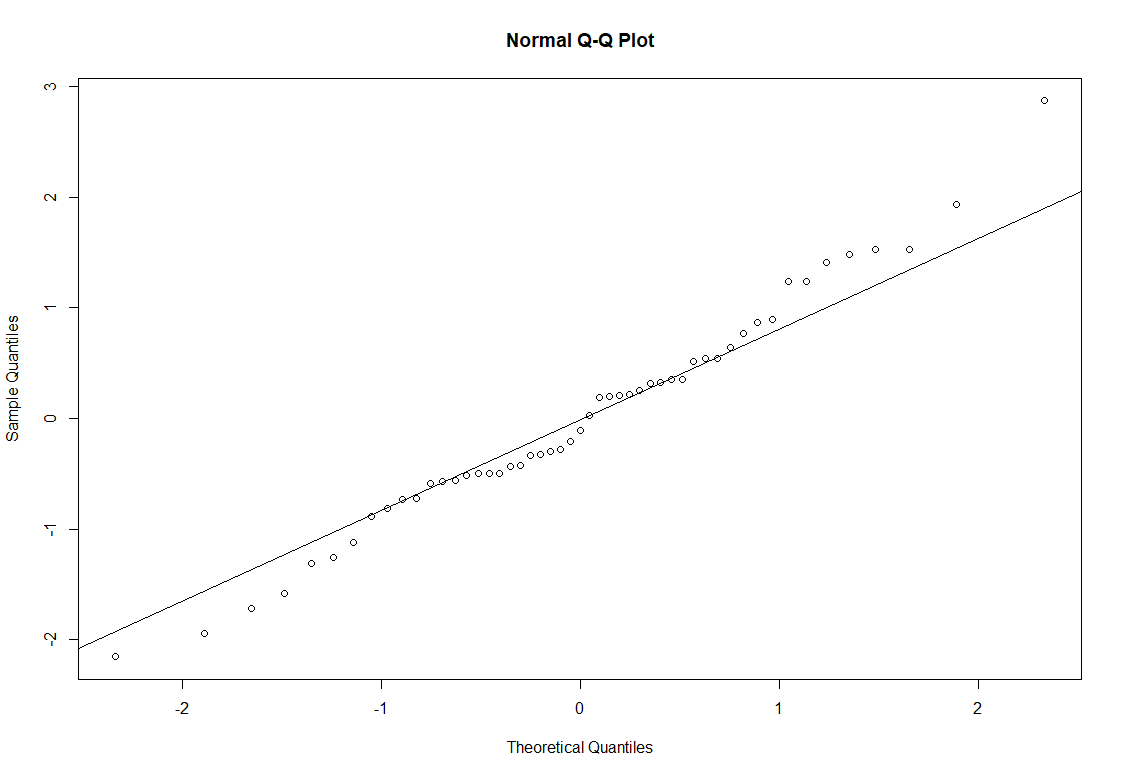
Hier kann man nun ganz gut erkennen, wie nah die Residuen an einer perfekten Normalverteilung dran sind. Abweichungen, speziell oben rechts und unten links sind nahezu immer zu beobachten, aber kein Grund zur Besorgnis. Die überwiegende Menge an Punkten liegt sehr nah an der Gerade und bisweilen auch darauf. Auch hiermit erkennt man eine hinreichende Normalverteilung der Residuen, was das Weiterrechnen der linearen Regression gestattet.
4 Normalverteilung in R testen: Analytische Methode
Als analytischen Test verwendet man – sofern man überhaupt analytisch testet (Hinweis unten beachten), den Shapiro-Wilk-Test. Dieser Test geht in seiner Nullhypothese davon aus, dass Normalverteilung der Daten vorliegt. Es sollte also das Ziel sein, die Nullhypothese nicht verwerfen zu können. Hierfür ist es notwendig, dass der Signifikanzwert (sog. p-Wert) über 0,05 liegt. shapiro.test() ist der Befehl hierfür:
shapiro.test(rstandard(model))
Das Ergebnis Tests ist relativ nüchtern gehalten:
Shapiro-Wilk normality test
data: rstandard(model)
W = 0.98481, p-value = 0.7532
Im Ergebnis ist anhand des sehr großen p-Wertes von 0,7532 ein Verwerfen der Nullhypothese von Normalverteilung nicht möglich. Es wird daher von Normalverteilung der Residuen ausgegangen.
ACHTUNG: Der Shapiro-Wilk-Test, wie auch der hier nicht gezeigte Kolmogorov-Smirnov-Test, kann zu fehlerhaften Aussagen führen. Warum und was man dagegen tun kann, zeige ich in diesem Artikel ausführlich.
5 Videotutorial


