Inhaltsverzeichnis
1 Ziel der multiplen linearen Regression
Eine multiple lineare Regression einfach erklärt: Sie hat das Ziel eine abhängige Variable (y) mittels mehrerer unabhängiger Variablen (x) zu erklären. Es ist ein quantitatives Verfahren, das zur Prognose einer Variable dient, wie das Beispiel in diesem Artikel zeigt.
Bei lediglich einer x-Variable wird die einfache lineare Regression gerechnet (SPSS,R, Excel). Habt ihr eine Moderation bzw. einen Interaktionseffekt, ist dies gesondert zu modellieren. Im Artikel Regression mit binären Variablen zeige ich das Rechnen und die Interpretation von binären unabhängigen Variablen bzw. Dummies im Rahmen der Regression.
2 Voraussetzungen der multiplen linearen Regression
Die wichtigsten Voraussetzungen sind, und werden in jeweils verlinkten Artikeln separat gezeigt:
- linearer Zusammenhangg zwischen x-Variablen und y-Variable
- metrisch skalierte y-Variable (mitunter ist auch ordinal vertretbar – da gibt es große Diskussionen zu :-D) – bei binär codierter y-Variable ist eine binär logistische Regression zu rechnen
- keine Multikollinearität – Korrelation der x-Variablen sollte nicht zu hoch sein
- normalverteilte Fehlerterme (=Residuen) – Achtung beim analytischen Testen mit Kolmogorov-Smirnov und Shapiro-Wilk-Test
- Homoskedastizität – homogen streuende Varianzen des Fehlerterms (grafische Prüfung oder analytische Prüfung)
- Optional: fehlende Werte definieren, fehlende Werte identifizieren und fehlende Werte ersetzen
- Kontrolle für einflussreiche Fälle bzw. “Ausreißer”
Im Vorfeld der Regressionsanalyse kann zudem eine Filterung vorgenommen werden, um nur einen gewissen Teil der Stichprobe zu untersuchen, bei dem man am ehesten einen Effekt erwartet.
3 Durchführung der multiplen linearen Regression in SPSS
Über das Menü in SPSS: Analysieren > Regression > Linear
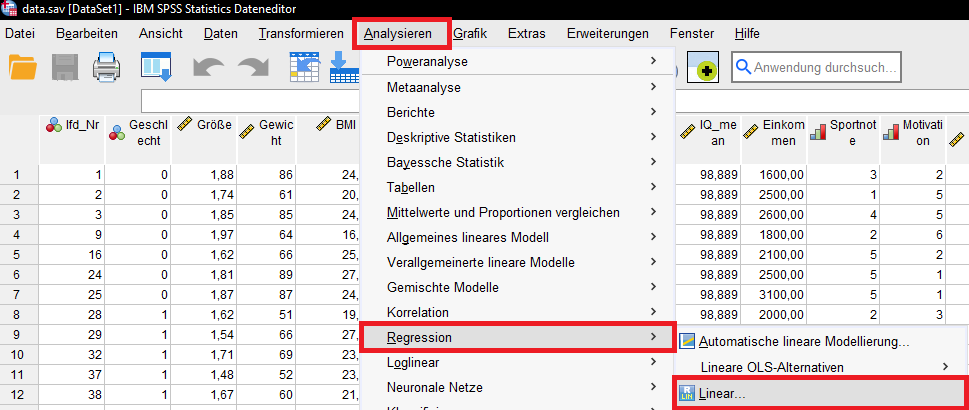
Das von mir gewählte Beispiel versucht die Zufriedenheit von Personen durch deren Einkommen, BMI und Geschlecht zu erklären. Die abhängige (y-)Variable (im Bild: 1) ist also die Zufriedenheit und die unabhängigen (x-)Variablen (im Bild: 2) das Einkommen, der BMI und das Geschlecht.
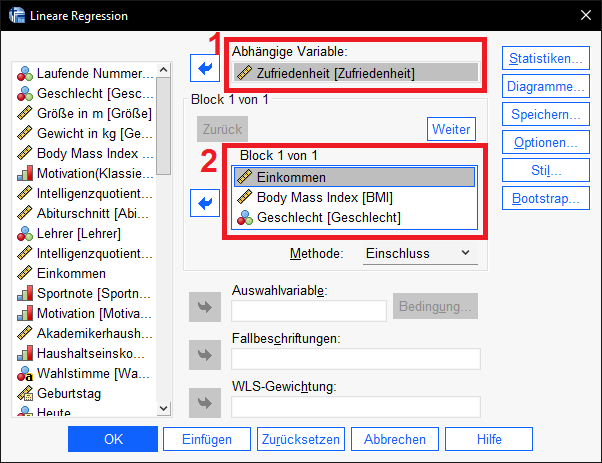
Hinweis: Das Geschlecht ist eine kategoriale Variable und besitzt im Datensatz die zwei Ausprägungen weiblich und männlich. Bei mehr als zwei Ausprägungen von kategorialen Variablen sind diese zwingend als Dummies zu kodieren. Ein anderer Beitrag behandelt die Interpretation von Dummies im Rahmen der linearen Regression in SPSS.
4 Beispiel von Ergebnistabellen der multiplen linearen Regression in SPSS
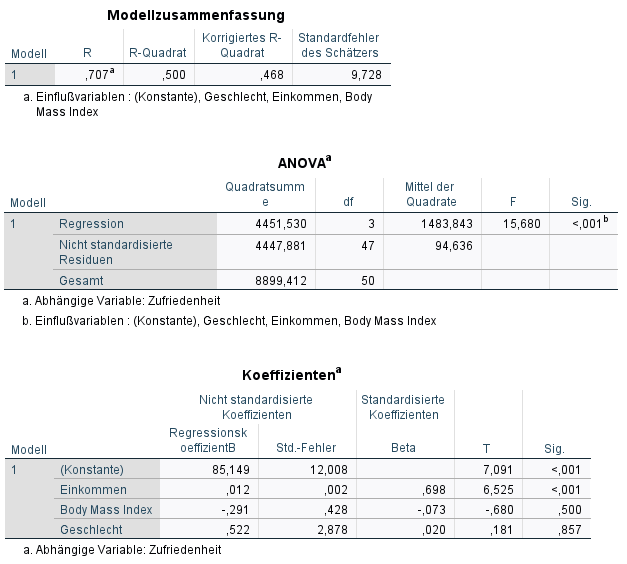
5 Interpretation der Ergebnisse der multiplen linearen Regression in SPSS
Sofern die in Gliederungspunkt 2 genannten Voraussetzungen erfüllt sind, sind drei Dinge besonders wichtig.
5.1 ANOVA-Tabelle – Signifikanz des F-Tests
Die ANOVA-Tabelle sollte einen signifikanten p-Wert (typischerweise <0,05) für den F-Test bei “Sig.” ausweisen – ist dies gegeben, leistet das Regressionsmodell einen Erklärungsbeitrag. Die Nullhypothese lautet beim F-Test: kein signifikanter Erklärungsbeitrag durch das Modell. Sie wird bei p < 0,05 verworfen. Im Beispiel ist die Signifikanz mit < 0,001 definitiv klein genug und damit leistet das spezifizierte Regressionsmodell einen (signifikanten) Erklärungsbeitrag.
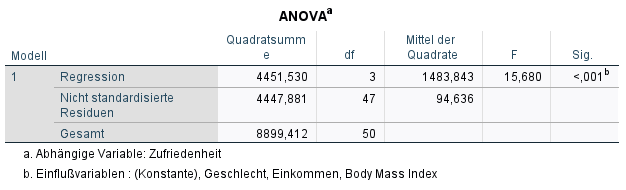
Hinweis: Mit Doppelklick auf den p-Wert erhält man den exakten Wert (3,3467E-7). Das ist die wissenschaftliche Schreibweise und E-7 bedeutet, dass das Komma um 7 Stellen nach links versetzt wird. Folglich: p = 3,3467E-7 = 0,00000033467 , was mit p < 0,001 abgekürzt wird.
![]()
![]()
5.2 Güte des Regressionsmodells
Die Modellgüte wird im multiplen Kontext anhand des normalen R-Quadrat (R²) und korrigierten R-Quadrat (korr. R²) abgelesen (im Beispiel: 0,500 bzw. 0,468). Beide findet man in der Tabelle Modellzusammenfassung.
Das R² ist zwischen 0 und 1 definiert. Es gibt an, wie viel Prozent der Varianz der abhängigen Variable erklärt werden. Ein höherer Wert ist hierbei besser. Bei einem R² von z.B. 0,5 werden 50% der Varianz der y-Variable (die Zufriedenheit) erklärt.

Das korrigierte R² ist nötig, weil mit einer größeren Anzahl an unabhängigen Variablen das normale R² automatisch steigt. Somit ist das korrigierte R² für Vergleiche zu anderen Modellen mit der gleichen abhängigen Variable sinnvoller. Das korrigierte R² ist stets niedriger als das normale R².
Pauschal gibt es in der multiplen linearen Regression keine Werte, ab denen man von einem “guten Modell” spricht. Vielmehr ist dies je nach Fachdisziplin unterschiedlich. Höher ist zwar pauschal besser, je mehr potenzielle Einflussfaktoren aber existieren, desto weniger können wenige einzelne Variablen erklären.
Die Zufriedenheit kann – abstrahiert von diesem fiktiven Datensatz – eben nicht nur durch Einkommen, BMI und Geschlecht versucht zu erklärt werden. Weitere Faktoren wie Wohnort, Arbeitszeiten, Kinder, Partnerschaft etc. sind denkbar.
5.3 Interpretation der Regressionskoeffizienten
A)Ist der jeweilige Regressionskoeffizient signifikant, also dessen p-Wert kleiner einem vorher definierten Alpha (typisch: 0,05), kann man die Nullhypothese für den jeweiligen Koeffizienten verwerfen.
Die Nullhypothese geht jeweils von keinem Effekt von der x auf die y-Variable aus.
Die Verwerfung der Nullhypothese bekräftigt demnach die Unterstellung eines Effektes von z.B. Einkommen auf Zufriedenheit.
Im Beispiel zeigt sich nur bei der Variable Einkommen eine Signifikanz, da p < 0,001 ist und damit unter der von mir im Vorfeld gesetzten Grenze von 0,05 liegt.
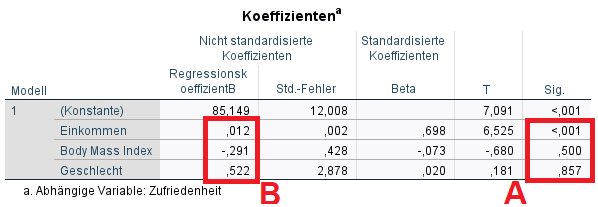
B)
Unter “Nicht standardisierte Koeffizienten” ist der Regressionskoeffizient B zu sehen. Hier ist zunächst nur jeweils B für signifikante x-Variablen interessant.
Im Beispiel wäre das lediglich bei “Einkommen” der Fall, welcher 0,012 beträgt.
Eine zusätzliche Einheit des Einkommens (1€ mehr) führt demnach zu einer zusätzlichen Zufriedenheit von 0,012.
Wäre B für das Einkommen fiktiv –0,012, würde eine Zunahme der Einheit “Einkommen” zu einer Abnahme der Zufriedenheit um 0,012 führen.
Steigere ich x um 1 Einheit, verändert sich y um B-Einheiten.
Da das Einkommen im Datensatz zwischen 1400 und 5600 und der BMI zwischen 16,49 und 33,9 liegt, kann anhand des nicht standardisierten Koeffizienten nicht gesagt werden, welcher Koeffizient einen größeren Einfluss hat – jeweilige Signifikanz vorausgesetzt!
Zum Vergleich zwischen signifikanten und nur signifikanten Variablen unterschiedlicher Wertebereiche dienen die standardisierten Koeffizienten (Beta). Anhand derer sieht man, welche x-Variable den größten positiven/negativen Einfluss auf die y-Variable hat. Man betrachtet hierbei stets den Betrag (z.B. |-0,073| = 0,073), also den positiven Wert des Koeffizienten.
Erneut der Hinweis: nicht signifikante Koeffizienten werden nicht berichtet bzw. interpretiert.
Wäre exemplarisch der BMI signifikant, könnte man anhand des Betrages des standardisierten Koeffizienten von 0,073, im Vergleich zum standardisierten Koeffizienten von 0,698 für das Einkommen schließen, das Einkommen die “wichtigere” Variable ist, weil sie den potentiell größeren Einfluss (Faktor 10) auf die Zufriedenheit ausübt.
Als Dummy codierte kategoriale Variablen haben zwar ebenfalls einen standardisierten Koeffizienten, welcher aber nicht interpretiert wird, auch wenn einen Signifikanz vorliegt!
Ein letzter technischer Hinweis: Teilt man B durch den Standardfehler (Std.-Fehler), erhält man den T-Wert (BMI: -0,291/0,428 = -0,680). Aus dem T-Wert wird letztlich der p-Wert ermittelt. Man kann sich merken, dass t-Werte >3 einen p-Wert < 0,05 zur Folge haben.
6 Prognose mittels Regressionsgleichung
Anhand der ersten Spalte der Koeffiziententabelle kann eine Regressionsgleichung aufgestellt werden. Die Signifikanz der Koeffizienten spielt hier KEINE Rolle.Es wird das B der Konstante und das Produkt aus x-Variablen und B’s addiert:
![]()
Im Beispiel lautet sie:
![]()
Bei einer Prognose kann man nun einen beliebigen Wert für Einkommen, BMI und Geschlecht einsetzen. Im Datensatz wurde Geschlecht dummycodiert mit 0=männlich, 1=weiblich. Setzt man z.B. ein Einkommen von 3000€, einen BMI von 25 und ein Geschlecht von 1 in diese Gleichung ein, erhält man auf Basis des Modells eine geschätzte Zufriedenheit von 114,396:
![]()
Hinweis: Solche Prognosen sind in ihrer Aussagekraft auf die zugrundeliegende Stichprobe eingeschränkt! Je besser die Stichprobe die Grundgesamtheit repräsentiert, desto eher kann für eine allgemeingültige Prognosekraft durch das geschätzte Modell argumentiert werden.
7 Ergebnistabelle für Berichte/Arbeiten
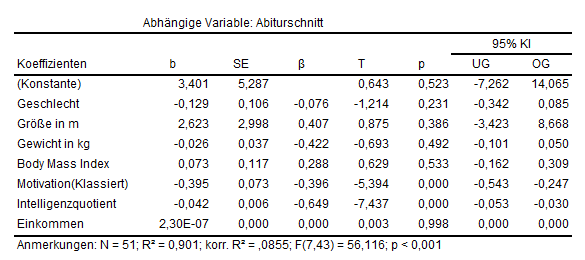
Um ein schönes Format der Tabelle und aller wesentlichen zu berichtenden Zahlen zu generieren, habe ich eine .xlsx-Vorlage gebaut. Alles weitere dazu findet ihr hier. Ein Beispiel einer anderen Regression könnte so aussehen:
8 Videotutorial
9 Beispieldatensatz für SPSS
10 Literatur
- Field, A. (2018), Discovering Statistics Using IBM SPSS Statistics, SAGE, Kapitel 9
- Warner, R. M. (2013), Applied Statistics, SAGE, kapitel 9, 11, 14
Weitere nützliche Tutorials findest du auf meinem YouTube-Kanal.


