Inhaltsverzeichnis
1 Was ist Multikollinearität?
Multikollinearität ist im Kontext der multiplen linearen Regression eine zu hohe Korrelation von zwei oder mehr erklärenden Variablen (x-Variablen) miteinander vorliegt. Wenn dem so ist, könnte man die inhaltliche Frage stellen, ob zwei miteinander hoch korrelierte unabhängige Variablen nicht sogar dasselbe messen und damit ein Weglassen einer der beiden denkbar wäre.
2 Was hat Multikollinearität für Folgen?
Die Regressionskoeffizienten werden bei vorhandener Multikollinearität verzerrt geschätzt. Die übliche Interpretation eines Regressionskoeffizienten ist, dass er eine Schätzung des Effekts einer Änderung um eine Einheit der unabhängigen Variablen x1 auf die abhängige Variable y liefert, wobei die anderen unabhängigen Variablen konstant gehalten werden. Wenn x1 in hohem Maße mit einer anderen unabhängigen Variablen x2 korreliert ist, kann eine Konstanthaltung von x2 eben gerade nicht gelingen, um den Effekt der Änderung von x1 um eine Einheit zu schätzen. Ein weiteres Problem können nach oben verzerrte Standardfehler der Koeffizienten sein. Das kann dazu führen, dass die Nullhypothese fälschlicherweise beibehalten wird (Fehler 2. Art).
Fragen können unter dem verlinkten Video gerne auf YouTube gestellt werden.
3 Grafisches Erkennen von Multikollinearität in SPSS
Eine Diagnosemöglichkeit, die nur für einen ersten Eindruck taugt, ist eine grafische Prüfung – eine analytische Prüfung ist auch denkbar. Hierzu kann man alle im Regressionsmodell vorhandenen unabhängigen Variablen in eine Streudiagrammmatrix setzen. Sie bildet die Korrelation ab und man erkennt bedenkliche Zusammenhänge sehr gut durch einen recht deutlichen linearen Zusammenhang. Um eine Streudiagrammmatrix zu erstellen, geht ihr über Grafik -> Diagrammerstellung und wählt bei Streu-/Punktdiagramm die “Streudiagramm-Matrix” aus. Sämtliche unabhängige Variablen eures Regressionsmodells zieht ihr nun auf die x-Achse des Diagramms und lasst es euch erstellen. ACHTUNG: nur metrisch skalierte Variablen lassen sich in dieser Matrix abbilden. Habt ihr auch ordinale Variablen, springt ihr direkt zur analytischen Methode. Für ein Beispiel habe ich die Variablen Größe, Gewicht, BMI und Intelligenzquotient abtragen lassen:

Erwartungsgemäß korrelieren Größe und Gewicht recht gut miteinander sowie Gewicht und der Body Mass Index. Das ist nicht verwunderlich, sind größere Menschen ja automatisch schwerer und auch ein schwererer Mensch hat in der Regel einen größeren BMI. Alles in allem hat man aber hier keinen Grund zur Annahme, dass eine hohe Korrelation vorliegt. Hätte man folgendes Bild, wäre es aber bedenklich:
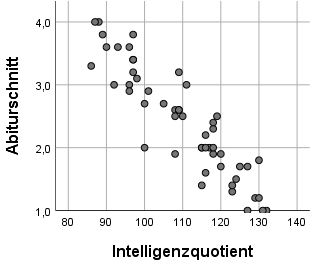
Bei der Korrelation von Intelligenzquotient und Abiturschnitt ist eine sehr starke (negative) Korrelation beobachtbar. Das ist auch logisch, da beide das Konstrukt Intelligenz messen können. Hier könnte man argumentieren, eine der beiden Variablen wegzulassen, sofern man beide in einem linearen Regressionsmodell gleichzeitig als unabhängige Variablen verwendet.
Zur genaueren Prüfung empfiehlt sich in jedem Falle eine analytische Diagnose, die ich in diesem Artikel ausführlich beschreibe.
4 Was tun bei Multikolliniearität?
Da sowohl Gewicht mit Größe als auch BMI in der Streudiagrammmatrix von oben eine recht hohe Korrelation hatte, habe ich entschieden, diese unabhängige Variable wegzulassen. Es ist wünschenswert und mitunter auch notwendig, inhaltlich zu argumentieren, dass im BMI das Gewicht ohnehin zur Berechnung herangezogen wird und dass größere Menschen sowieso meist schwerer sind – die Übergewichtigen mal vernachlässigt. Die neue Koeffiziententabelle ohne Gewicht als unabhängige Variable sieht dann wie folgt aus:
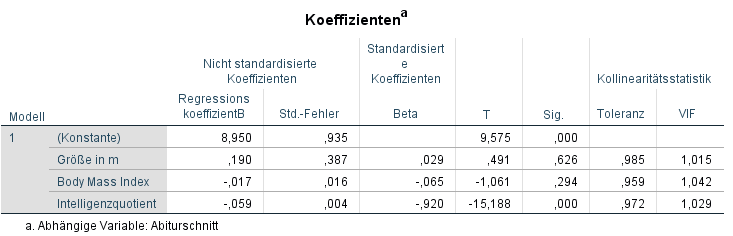
Hier ist erkennbar, dass das Löschen von Gewicht als unabhängige Variable im Regressionsmodell ein guter Schritt war. Die VIF-Werte (was das ist -> Artikel) sind alle nahe 1 und damit nicht annähernd nahe dem kritischen Wert von 10. Die Toleranz zeigt entsprechend der oben gezeigten Berechnungsvorschrift logischerweise keine Werte <0,1. Zusammengefasst ist das (inhaltlich) begründete Weglassen von unabhängigen Variablen mit einem hohen VIF-Wert zur Vermeidung von Multikollinearität der richtige Weg. Allein anhand der Streudiagrammmatrix und der Korrelationsmatrix sollte keine Entscheidung getroffen werden und zusätzlich auf die eben genannten Werte Bezug genommen werden. Das kann man hier noch mal in Ruhe nachlesen.
5 Videotutorial
6 Weiterführende Literatur
- Field, A. P., & Field, A. P. (2018). Discovering statistics using IBM SPSS statistics. London ; Thousand Oaks.
- Kutner, M. H. (2005). Applied linear statistical models. Boston: McGraw-Hill Irwin.


