Inhaltsverzeichnis
1 Ziel der Moderation in SPSS (Interaktion)
Eine Moderation (auch Interaktion) unterstellt den Einfluss einer zusätzlichen Variable (=Moderator) auf eine Beziehung zwischen einer unabhängigen Variable (X) und einer abhängigen Variable (Y). Dieser Artikel zeigt, wie man dies in SPSS modelliert und berechnet. Eine Anleitung, für eine deutlich bequemere Rechnung der Moderation mit PROCESS gibt es hier.
2 Voraussetzungen der Moderation (Interaktion)
Die wichtigsten Voraussetzungen sind:
- linearer Zusammenhang zwischen x-Variablen und y-Variable
- metrisch skalierte y-Variable (mitunter ist auch ordinal vertretbar – da gibt es große Diskussionen zu :-D)
- keine Multikollinearität – Korrelation der x-Variablen sollte nicht zu hoch sein
- normalverteilte Fehlerterme – Achtung beim analytischen Testen mit Kolmogorov-Smirnov und Shapiro-Wilk-Test
- Homoskedastizität – homogen streuende Varianzen des Fehlerterms (grafische Prüfung oder analytische Prüfung)
- keine Autokorrelation – Unabhängigkeit der Fehlerterme (Vorsicht bei Durbin-Watson-Test!) – nur bei Daten relevant, wo eine zeitliche Reihenfolge existiert
- Optional: fehlende Werte definieren, fehlende Werte identifizieren und fehlende Werte ersetzen
3 Das Prinzip der Moderation
Eine Moderation, auch Interaktion genannt, unterstellt einen moderierenden Einfluss einer Variable (M) auf einen Zusammenhang zwischen zwei Variablen (X->Y).
Als Beispielt hängt der Abiturschnitt (Y) nicht allein von der Intelligenz (X) ab. Vielmehr beeinflusst die Motivation (M) den Einsatz der Intelligenz, um einen gewissen Abiturschnitt zu erreichen. Konkret sieht das in folgender Abbildung so aus:
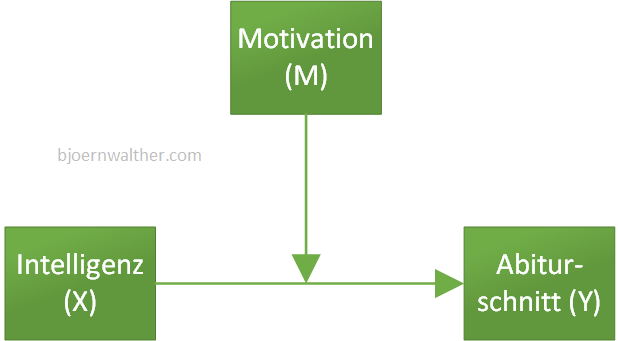
Da SPSS keine Möglichkeit bietet, eine Moderation direkt zu modellieren, muss eine Umwandlung bzw. Transformation vorgenommen werden. Der Moderator (M), die unabhängige Variable (X) als auch der Interaktionseffekt (X*M) werden gleichzeitig als unabhängige Variablen aufgenommen. Dies zeigt die folgende Abbildung:
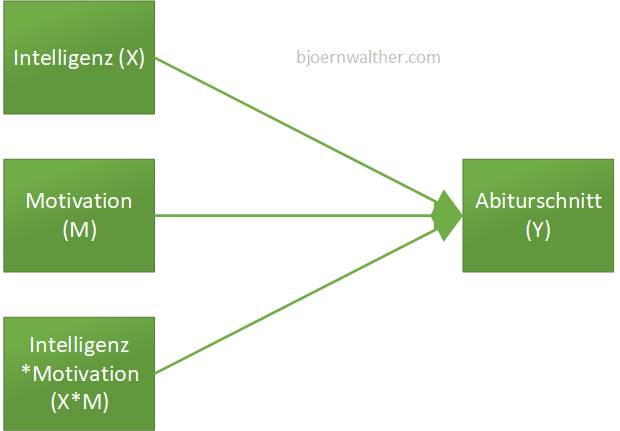
4 Durchführung der Moderation in SPSS
4.1 Bildung des Interaktionsterms
Wie in obiger Abbildung ersichtlich, ist neben X und M noch ein Interaktionsterm (X*M) zu bilden, der das Produkt von X und M darstellt. Das funktioniert über „Transformieren“ > „Variable berechnen“. Im Beispiel wird als Zielvariable „Intelligenz_x_Motivation“ festgelegt. Sie setzt sich aus Intelligenz (mit IQ abgekürzt) mal Motivation zusammen:
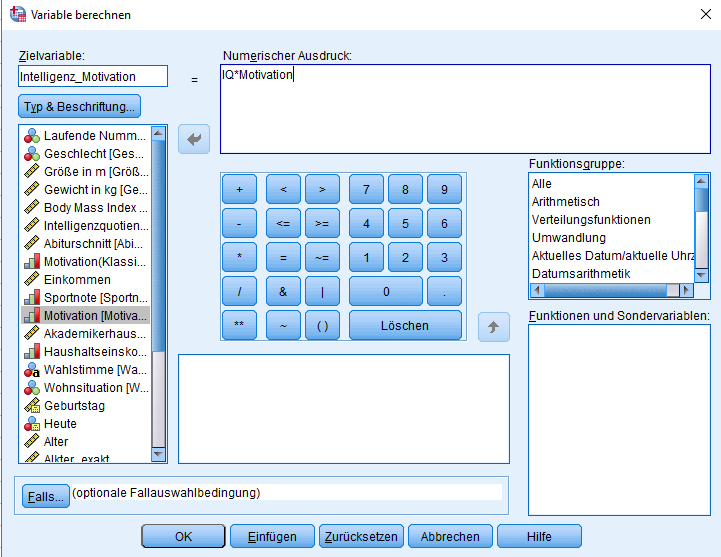
In der Datenansicht erscheint nun eine neue Variable am Ende der Datei, die entsprechend den Namen der Zielvariable trägt und das Produkt eurer Variablen X und M darstellt.
Die immer wieder Fragen bzgl. Standardisierung aufkommen, hier noch ein Hinweis aus Hayes (2018), S. 525: „Fourth, as with mean centering, the decision to standardize X and W or to report standardized or unstandardized regression coefficients is your choice to make. But if you choose to do so, don’t say you are doing so to reduce the effects of collinearity. Personally, I prefer to talk about regression results in unstandardized form. […] When doing so, make sure that you are reporting and interpreting the coefficients corresponding to the unstandardized model in the output of your program and not the standardized model. Indeed, as a general rule, never report or interpret the coefficients listed in a standardized section of the output when your model includes the product of two variables along with the components of that product, and don’t use these coefficients to probe an interaction.“
4.2 Rechnen der Moderation
Nach dem Bilden des Interaktionsterm führt man wie gewohnt eine multiple lineare Regression in SPSS durch.
Über „Analysieren“ > „Regression“ > „Linear“
Die Variablen X, M und X*M werden wie gewohnt in die Box „unabhängige Variablen“ abgelegt, die Y-Variable wird als abhängige Variable festgelegt.
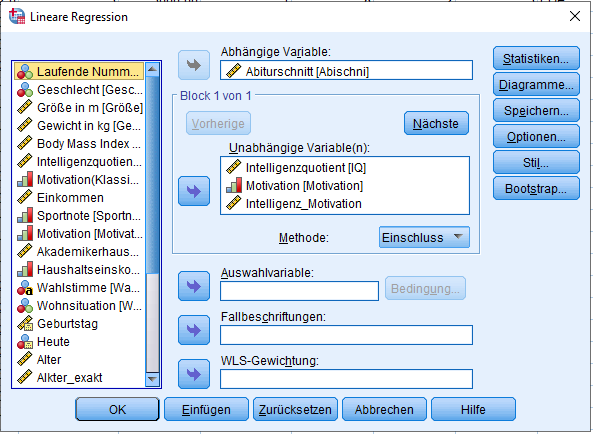
Mit OK wird die Moderation in SPSS berechnet und führt zu den folgenden Ergebnistabellen.
5 Beispiel von Ergebnistabellen der Moderation in SPSS
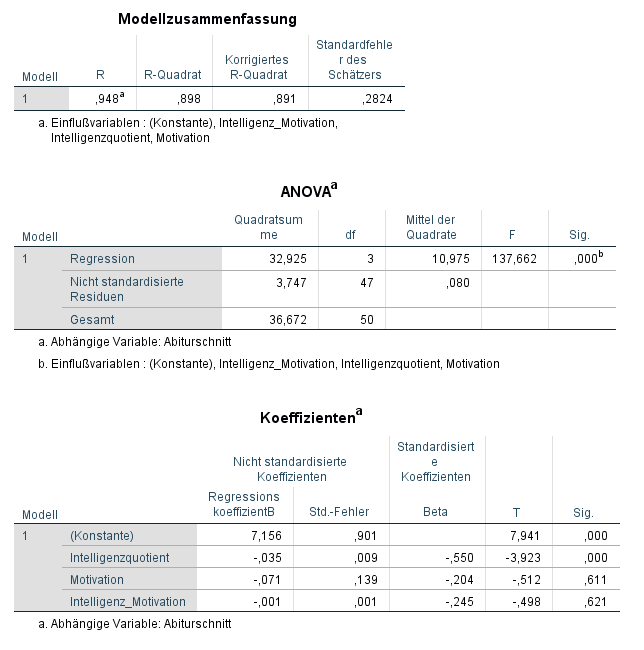
Nach der entsprechenden Durchführung erhaltet ihr drei Tabellen.
6 Interpretation der Ergebnisse der multiplen linearen Regression in SPSS
Sofern die o.g. Voraussetzungen erfüllt sind, sind drei Dinge bei der Ergebnisinterpretation bei der multiplen Regression besonders wichtig.
6.1 ANOVA-Tabelle
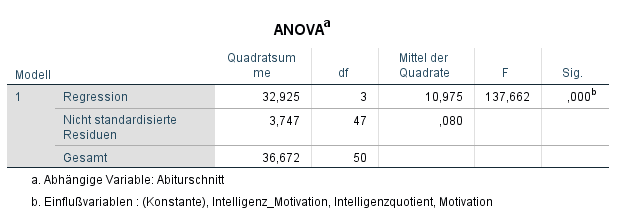
Der F-Test in der ANOVA-Tabelle sollte in der Zeile „Regression“ einen signifikanten Wert (<0,05) ausweisen – ist dies der Fall, leistet das aufgestellte Regressionsmodell einen Erklärungsbeitrag. Im Beispiel oben ist die Signifikanz < 0,001 und damit <0,05. Dies bedeutet, dass alles in Ordnung ist: Die Nullhypothese des F-Tests (Modell leistet keinen Erklärungsbeitrag) wird entsprechend verworfen.
Ist die Signifikanz allerdings >0,05, muss an dieser Stelle die multiple lineare Regression bzw. deren Berechnung abgebrochen werden. Warum? Weil das multiple Regressionsmodell mit seinen unabhängigen Variablen schlicht die abhängige Variable nicht besser erklären kann als ohne. Meist ist dies ein Hinweis auf keine hinreichende Linearität des Zusammenhanges, sofern es eine hinrechend große Stichprobe (n > 30) ist.
6.2 Die Modellgüte
Die Modellgüte wird anhand des korrigierten R-Quadrat (R²) abgelesen (im Beispiel: 0,891). Dies findet man in der Tabelle Modellzusammenfassung. Korrigiert ist es deswegen, weil mit einer größeren Anzahl an unabhängigen Variablen das normale R² automatisch steigt. Das korrigierte R² kontrolliert hierfür und ist deshalb stets niedriger als das normale R². Sowohl normales als auch korrigiertes R² sind zwischen 0 und 1 definiert. Nur das normale R² (hier 0,898) gibt an, wie viel Prozent der Varianz der abhängigen Variable erklärt werden. Höher ist dabei besser. Bei einem R² von 0,898 werden 89,8 % der Varianz der y-Variable erklärt.
Hinweis: Ein R² von fast 0,9 ist ein sehr hoher Wert, was bei diesem konstruierten Beispiel nicht verwunderlich ist. Ein deutlich niedrigeres R² ist je nach Kontext eher die Regel als die Ausnahme.
6.3 Koeffiziententabelle
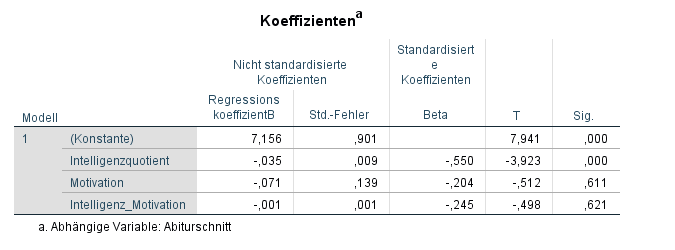
Die Regressionskoeffizienten sollten signifikant (p < 0,05) sein. Im Beispiel ist dies nur der Intelligenzquotient. Unter „nicht standardisiert“ ist der interpretierbare Effekt dieses Koeffizienten zu sehen. Im Beispiel ist der Koeffizient vom Intelligenzquotient -0,035. Das heißt, mit jeder zusätzlichen Einheit (jeder IQ-Punkt) dieser x-Variable, ist eine Abnahme von 0,035 Einheiten der y-Variable (Abiturschnitt) verbunden. Somit wirkt sich Intelligenz gut auf die Abiturnote aus. Positive Koeffizienten wirken sich entsprechend schlecht auf die Abiturnote aus. Die Motivation selbst ist aufgrund des hohen Signifikanzwertes von p = 0,611 kein Einflussfaktor auf die Abiturnote.
Zum Vergleich zwischen signifikanten Variablen dienen die standardisierten Koeffizienten. Anhand derer sieht man, welcher den größten positiven/negativen Einfluss auf die y-Variable hat. Man betrachtet stets den Betrag (z.B. |-0,550| = 0,550), also den positiven Wert des Koeffizienten.
6.4 Der Interaktionseffekt
Der Interaktionseffekt von Intelligenz und Motivation ist in diesem Beispiel mit einer Signifikanz von p = 0,621 kein signifikanter Prädiktor für die Abiturnote. Die Motivation verstärkt also weder den Einfluss der Intelligenz auf die Abiturnote, noch schwächt sie den Einfluss ab.
Angenommen der Interaktionseffekt also der Koeffizient „Intelligenz_x_Motivation“ wäre signifikant, dann würde der negative Koeffizient (-0,001) die negative Wirkung der X-Variable (Intelligenz) auf die Y-Variable (Abiturnote) noch weiter negativ verstärken. Im Beispiel würde das bedeuten, dass eine höhere Ausprägung der Motivation den Effekt des IQ verstärkt. Zusammengenommen sind hohe Werte von Motivation und IQ für eine bessere Abiturnote verantwortlich als alle anderen Kombinationen (niedrige Motivation + hoher IQ, niedrige Motivation + niedriger IQ). Dies könnte man grafisch ermitteln, wenn man eine einfache Regressionsgleichung mit der Konstanten und allen Koeffizienten aus der Koeffiziententabelle aufstellt:
y = 7,156 – 0,035*Intelligenzquotient – 0,071*Motivation – 0,001*Intelligenz_x_Motivation. Dies kann man für verschiedene plausible Ausprägungen von X (Intelligenzquotient: 80, 100, 120, 140, 160) und M (Motivation: 2,4,6,8,10) durchführen und sich entsprechende Regressionsgeraden zeichnen lassen. Am einfachsten funktioniert dies in Excel und führt zu folgender Grafik:
Erneut der Hinweis: mit PROCESS erhält man eine Syntax zur 1-Klick-Generierung einer solchen Grafik
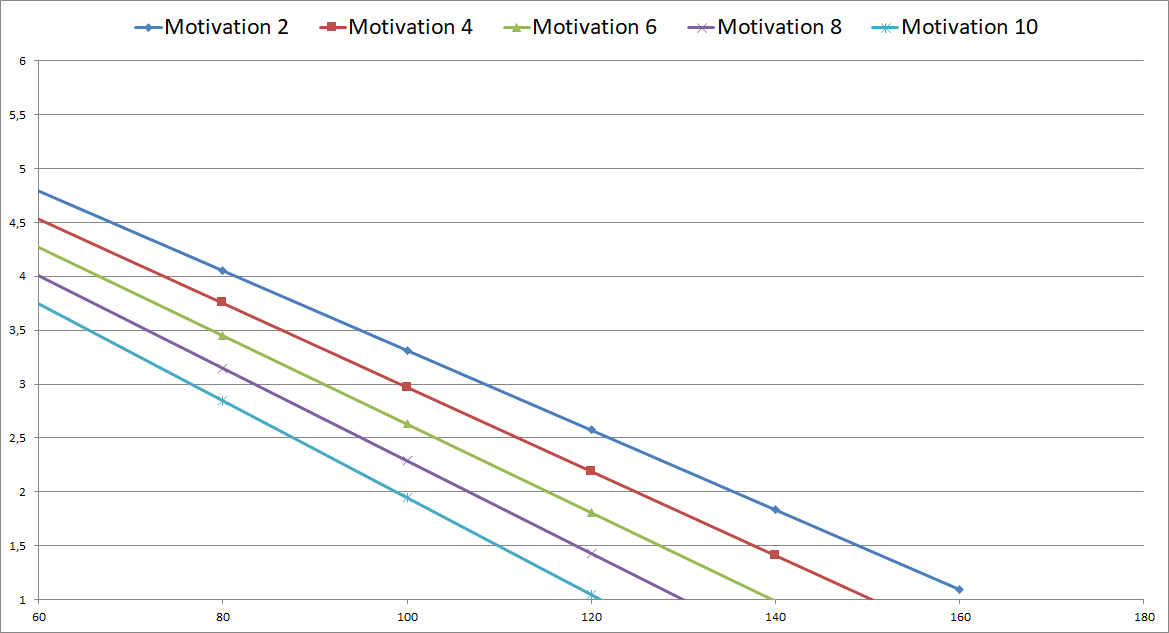
Hier erkennt man recht deutlich, dass ein IQ von 120 mit einer Motivation von 10 auf den gleichen Abiturschnitt kommt wie ein IQ von 160 mit einer Motivation von 2, nämlich 1,0. Es ist erkennbar, dass mit zunehmender Motivation (Geraden befinden sich weiter links), ein geringerer IQ notwendig ist, um den gleichen Abiturschnitt zu erzielen. Gleichzeitig sinkt der Abiturschnitt mit steigender Motivation bei gleichbleibender Intelligenz stärker.
7 Videotutorial
8 Literatur
- Hayes, A. F. (2018). Introduction to Mediation, Moderation, and Conditional Process Analysis: A Regression-Based Approach. USA: Guilford Publications.
