Inhaltsverzeichnis
1 Ziel des Levene-Tests
Ein Levene-Test (in Form eines F-Tests) prüft anhand der F-Verteilung, ob zwei oder mehr Gruppen verschiedene Varianzen haben oder Varianzgleichheit existiert. Hierbei sollten die Gruppen keine stark unterschiedlichen Umfänge haben, da die F-Statistik für den Test sonst verzerrt ist. Die Nullhypothese lautet, dass sie gleiche Varianzen besitzen. Die Alternativhypothese demzufolge entsprechend, dass sie unterschiedliche Varianzen besitzen. Der Levene-Test kann auch in SPSS oder R berechnet werden.
Voraussetzungen für einen Levene-Test sind 1) in etwa normalverteilte Daten und 2) unabhängige Stichproben/Gruppen. Wie Daten auf Normalverteilung geprüft werden, zeige ich hier.
2 Durchführung des Levene-Tests in Excel
Eine vorgefertigte Funktion des Levene-Tests gibt es in Excel im Datenanalyse-Funktionsbereich. Allerdings kann man den Test auch recht einfach in Excel “nachbauen” und ein Testergebnis erhalten. Es braucht nur die Varianzen
Zunächst sind die Stichprobenvarianzen zu berechnen. Ich runde nachfolgend bei allen Berechnungen auf 2 Nachkommastellen. Die Berechnung der Stichprobenvarianz erfolgt mir der “VAR.S()“-Funktion. Im Beispiel berechne ich Varianz I für die obere Gruppe (Training=2) und erhalte den Wert 94,81. Die untere Gruppe (Training=0) hat die Varianz II und einen Wert 92,17.
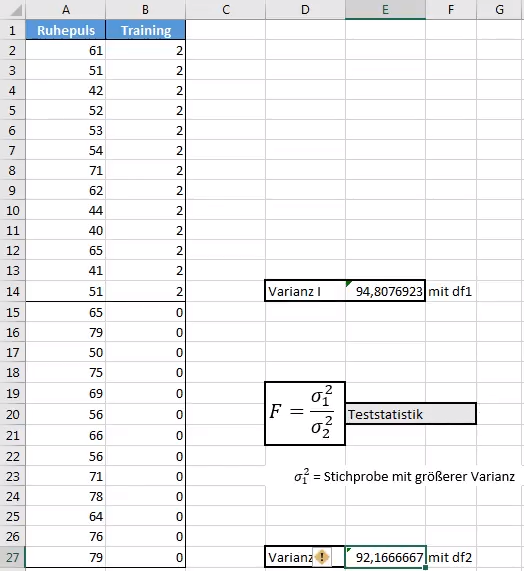
Im nächsten Schritt ist aus Varianz I und II ein Quotient zu bilden. Es ist dabei wichtig, dass die größere Varianz im Zähler des Bruches steht. Der Quotient ist die sog. Teststatistik (grau unterlegt im Bild oben). 94,81 geteilt durch 92,17 ergibt eine Teststatistik von 1,03. Diese Teststatistik muss mit dem kritischen Wert verglichen werden. Per Augentest sind Quotienten nahe 1 meist schon ein ausreichender Indikator für Varianzgleichheit.
3 Kritischer Wert im Levene-Test – Berechnung
Der kritische Wert, dem die Teststatistik gegenübergestellt wird, wird mit der F-Verteilung ermittelt. Genauer gesagt nutzt man hierzu die Funktion F.INV(). Sie gibt Quantile der F-Verteilung zurück. Wir lassen uns nun das 0,95 bzw. 95%-Quantil zurückgeben. Das sieht dann so aus:
=F.INV(0,95;12;12)
Die beiden 12en stehen hier für die Freiheitsgrade (df=degrees of freedom). Die ergeben sich aus der jeweiligen Gruppengröße abzüglich 1. Beide Gruppen sind im Beispiel gleich groß (13 Fälle). Daher ergeben sich df=13-1=12. Solltet ihr mal ungleiche Gruppengrößen haben, ist als erster Freiheitsgrad in der F.INV-Formel jener zu wählen, der zur Gruppe mit der höheren Varianz gehört.
Der kritische Wert für F.INV(0,95;12;12) ist 2,69.
4 Kritischer Wert vs. Teststatistik
Im Beispiel ist die Teststatistik 1,03 und wird mit dem kritischen Wert von 2,69 verglichen. Hier ist der Fall recht eindeutig. 1,03 ist deutlich kleiner als 2,69. Damit kann ich die Nullhypothese von Varianzgleichheit (Varianzhomogenität) mit dem Levene-Test nicht verwerfen. Die Varianzen sind also gleich bzw. ähnlich genug, dass ich z.B. einen t-Test für unabhängige Stichproben rechnen kann. Die Nullhypothese würde ich nur dann ablehnen, wenn die Teststatistik über 2,69 liegen würde. In dem Fall wäre ich die Alternativhypothese von Varianzungleichheit (Varianzheterogenität) annehmen.
5 Vorsicht – eingeschränkte Verwendbarkeit des Levene-Tests
Die Verwendung des Levene-Tests ist – wie jeder analytische Test – in großen Stichproben zu sensitiv bzw. reagiert auf unbedeutende Abweichungen von Varianzhomogenität zu sensibel. Demzufolge sollten die Ergebnisse kritisch betrachtet werden und im Zweifel bei großen Stichproben lieber auf eine Einschätzung der Varianz an sich geschaut werden (Field, A. (2018), S. 259).
6 Literatur zum Levene-Test
- Field, A. (2018): Discovering Statistics Using SPSS, 5. Auflage, Sage, London.
- Levene, H. (1960): Robust tests for equality of variances. Contributions to probability and statistics: 278–292, Stanford Univ. Press, Stanford, Calif.
7 Videotutorial
Weitere nützliche Tutorials findest du auf meinem YouTube-Kanal.


