Inhaltsverzeichnis
1 Ziel des Kruskal-Wallis-Test in SPSS
Der Kruskal-Wallis-Test ist ein nicht parametrischer Mittelwertvergleich bei mehr als 2 Stichproben bzw. Gruppen. Er verwendet Ränge statt die tatsächlichen Werte und ist das Gegenstück zur einfaktoriellen ANOVA, allerdings hat er nicht solche strengen Voraussetzungen.
2 Voraussetzungen des Kruskal-Wallis-Tests in SPSS
- mindestens drei voneinander unabhängige Stichproben/Gruppen
- ordinal oder metrisch skalierte y-Variable
- normalverteilte y-Variable innerhalb der Gruppen nicht nötig
3 Durchführung des Kruskal-Wallis-Tests in SPSS
Über das Menü in SPSS: Analysieren > Nichtparametrische Test > Unabhängige Stichproben
Im Reiter Variablen ist als Testvariable die zu testende Variable (hier Ruhepuls) einzusetzen. Die Gruppierungsvariable (hier: Training) ist die Variable, die die Gruppen unterscheidet. Im Beispiel testen wir untrainierte, mäßig trainierte und gut trainierte Menschen auf Unterscheide hinsichtlich ihres Ruhepulses.
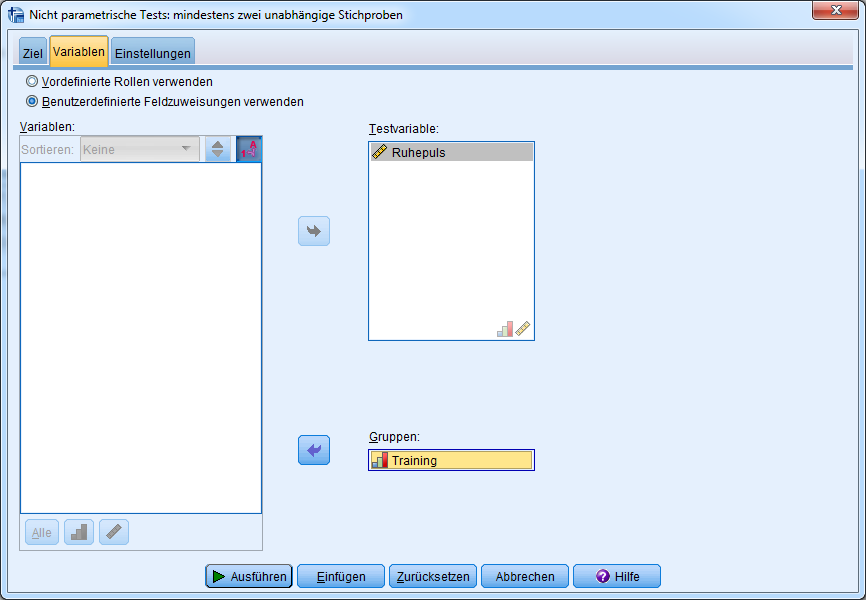
Im Reiter Einstellungen wird unter dem Element “Tests auswählen” die Option Tests anpassen gewählt. Rechts wird dann “einfaktorielle ANOVA nach Kruskal-Wallis (k-Stichproben)” selektiert. Bei Mehrfachvergleiche sollte “Alle paarweise” ausgewählt sein. Das hat den Hintergrund, dass wir wissen wollen, zwischen welchen der k Gruppen/Stichproben (hier: 3) ein statistisch signifikanter Unterschied des Mittelwertes besteht.
Für die Kumulierung des Alphafehlers infolge mehrfachen Testens derselben Gruppen wird eine Korrektur durchgeführt, indem die Signifikanz angepasst wird. Mehr dazu unten.
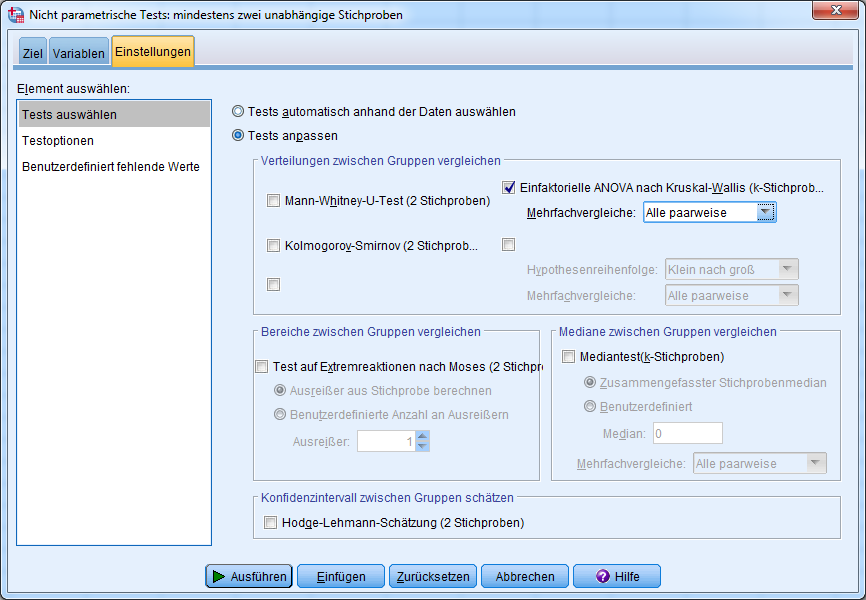
Ein Klick auf “Ausführen” führt die Berechnung durch und zeigt die Ergebnisse an.
4 Interpretation der Ergebnisse des Kruskal-Wallis-Test in SPSS

Die einzige Ausgabe, die man erhält, ist die Hypothesenübersicht. Hierbei wird die Signifikanz angezeigt (0,004) und was mit der Nullhypothese zu tun ist. Sie ist abzulehnen, da die Signifikanz unter dem typischen Alphawert von 0,05 liegt. Die Nullhypothese des Kruskal-Wallis-Test geht von gleichen bzw. ähnlichen mittleren Rängen aus. Die Alternativhypothese demzufolge von unterschiedlichen mittleren Rängen. Da wir die Nullhypothese verwerfen müssen, ist die Alternativhypothese anzunehmen. Für diese Stichproben konnte demnach gezeigt werden, dass es statistisch signifikante Unterschiede zwischen ihnen hinsichtlich des Ruhepulses gibt.
Als Nächstes ist ein Doppelklick auf diese Ausgabe durchzuführen. Es startet sich der “Modellviewer“. Hier wird standardmäßig für jede Gruppe ein Boxplot (ausführlicher Artikel zur Interpretation) zur Beschreibung der Verteilung erstellt sowie die Testwerte darunter gelistet. Es ist anhand des Boxplots erkennbar, dass der Median als auch die Quartile (die Box) mit dem Trainingsstand immer weiter sinkt – das, was man sich schon gedacht hat.
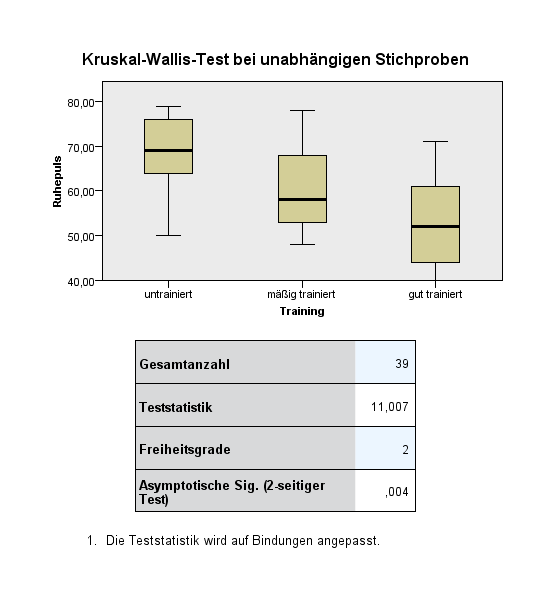
Die Daten der unteren Tabelle sind die Testergebnisse. Die Teststatistik ist 11,007 und muss normalerweise dem kritischen Wert gegenübergestellt werden, um die Nullhypothese zu prüfen. Allerdings kann man sich auch lediglich auf den p-Wert (0,004) beschränken – die einfachere Methode mit demselben Ergebnis.
5 Paarweise Vergleiche
Allerdings ist hiermit noch nicht gesagt, zwischen welchen der hier vorliegenden drei Gruppen ein statistisch signifikanter Unterschied vorliegt. Es gibt drei Gruppen, drei mögliche paarweise Vergleiche, die man sich anschauen muss.
- gut trainiert vs. mäßig trainiert
- gut trainiert vs. untrainiert
- mäßig trainiert vs. untrainiert
In der Fußzeile des Modellviewers gibt es im Punkt “Ansicht” die Option “Paarweise Vergleiche“. Diese ist auszuwählen und zeigt folgende Ergebnisse:
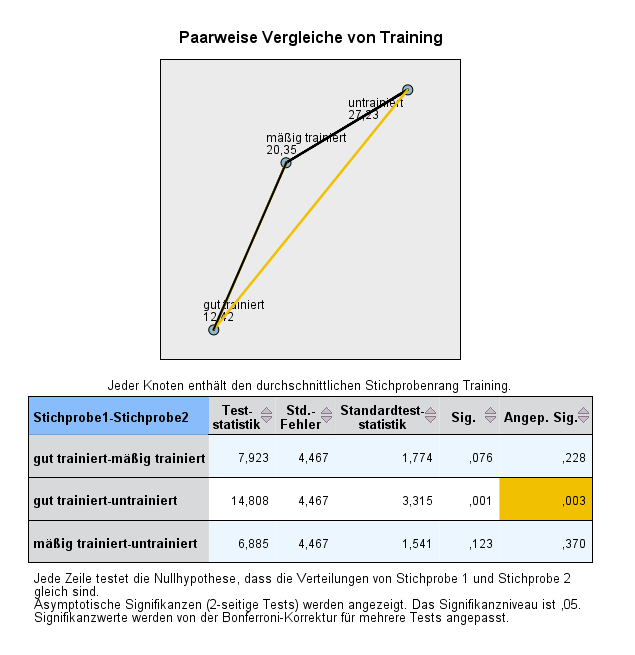
Die Grafik kann man ignorieren – sie zeigt nichts anderes als die Tabelle. Die orange Linie bzw. das orange Kästchen zeigt den einzigen statistisch signifikanten Unterschied bei den Gruppen. Es ist die Angepasste Signifikanz zu beurteilen, da wir mehrfach auf eine Stichprobe testen. Damit vermeidet man, dass infolgedessen von einem zu niedrigen Alphafehler ausgegangen und damit fälschlicherweise die Nullhypothese verworfen wird (Fehler 1. Art).
Im Ergebnis unterscheiden sich lediglich gut trainierte und untrainierte Menschen hinsichtlich ihres Ruhepulses. Die statistische Signifikanz liegt bei 0,003 und damit unter 0,05. Somit ist nun auch klar, welcher paarweiser Vergleich für den statistisch signifikanten Unterschied verantwortlich ist. In diesem konstruiertem Beispiel unterscheiden sich lediglich gut trainierte und untrainierte Menschen hinsichtlich ihres Ruhepulses.
6 Ermittlung der Effektstärke des Kruskal-Wallis-Tests
Die Effektstärke r wird jeweils für alle signifikanten paarweise Vergleiche mit folgender Formel berechnet. Der z-Wert (Standardteststatistik) wird durch die Wurzel der Stichprobengröße geteilt. Aufgrund der Betragsstriche wird dieser Quotient immer positiv sein. Eine Effektstärke kann man sinnvollerweise allerdings nur für statistisch signifikante Unterschiede berechnen. In diesem Beispiel für untrainierte und gut trainierte Menschen.
Eine Besonderheit ist bei der Berechnung noch zu beachten. n ist die Summe der Gruppengrößen, die man vergleicht. Da sowohl die Gruppe der gut trainierten als auch der untrainierten Menschen jeweils 13 ist, ist n=2*13 = 26.
![]()
Im Beispiel ist also der Betrag von -3,315 durch die Wurzel aus 26 zu teilen. Das Ergebnis hieraus lautet: 0,65.
Laut Cohen: Statistical Power Analysis for the Behavioral Sciences (1988), S. 79-81 sind die Effektgrenzen:
- ab 0,1: schwach,
- ab 0,3: mittel und
- ab 0,5: stark.
Im vorliegenden Beispiel ist die Effektstärke mit 0,65>0,5 stark. Es handelt sich also um einen starken Effekt hinsichtlich des Unterschiedes des Ruhepulses.
7 Literatur
- Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences, Routledge.
- Cohen, J. (1992). A power primer. Psychological bulletin, 112(1), 155.
- Kruskal, W. H., & Wallis, W. A. (1952). Use of ranks in one-criterion variance analysis. Journal of the American statistical Association, 47(260), 583-621.
8 Videotutorial
Weitere nützliche Tutorials findest du auf meinem YouTube-Kanal.


