Inhaltsverzeichnis
1 Ziel von Kolmogorov-Smirnov-Test und Shapiro-Wilk-Test
Sind für parametrische Tests wie z.B. dem t-Test oder der Regression die Daten bzw. Residuen auf Normalverteilung zu prüfen, macht man das typischerweise mit grafischen oder analytischen Tests. Letztere sind Kolmogorov-Smirnov-Test und Shapiro-Wilk-Test. Allerdings sind sie nicht uneingeschränkt zu empfehlen, wie dieser kurze Artikel zeigt.
2 Zwei Beispielverteilungen – deskriptive Daten
Ich habe zwei Variablen (V01 und V02) mit Verteilungen generiert, die standardnormalverteilt sind. Das heißt, ihr Mittelwert ist 0 und die Standardabweichung 1. Die Variablen umfassen jeweils 1000 Fälle. Es sind also verhältnismäßig sehr große Stichproben, was noch entscheidend sein wird. Hier sind zunächst die deskriptiven Statistiken der beiden Variablen, die auch bei Schiefe und Kurtosis unauffällig sind:

Die beiden Verteilungen sind also rein deskriptiv nicht bedenklich schief oder sonderlich steil, so dass man nicht von nicht normalverteilten Variablen ausgehen muss.
3 Zwei Beispielverteilungen – grafische Beurteilung
3.1 Histogramme
Zunächst sind hier die Histogramme zu sehen. Sie bilden die Ausprägungen und der Häufigkeiten ab. Beide Histogramme zeigen keine Auffälligkeiten. Im Gegenteil, sie bilden eine Normalverteilung sehr gut ab – zumindest für einen realen Anwendungsfall wäre das eine sehr gute Ausgangsbasis und es würde kein Grund bestehen, auf dieser Basis für ein nicht parametrisches Verfahren zu plädieren.
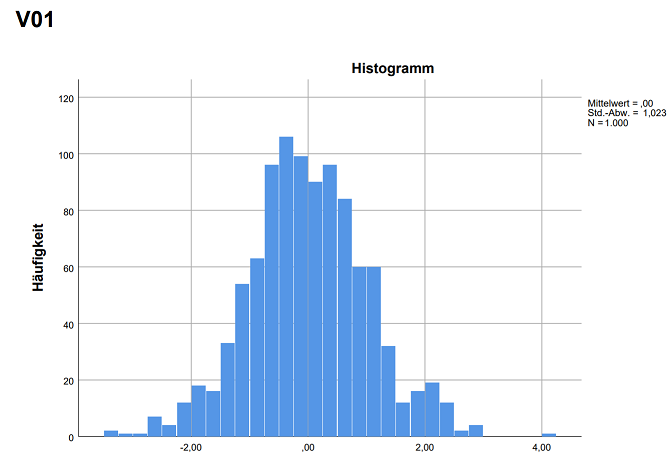
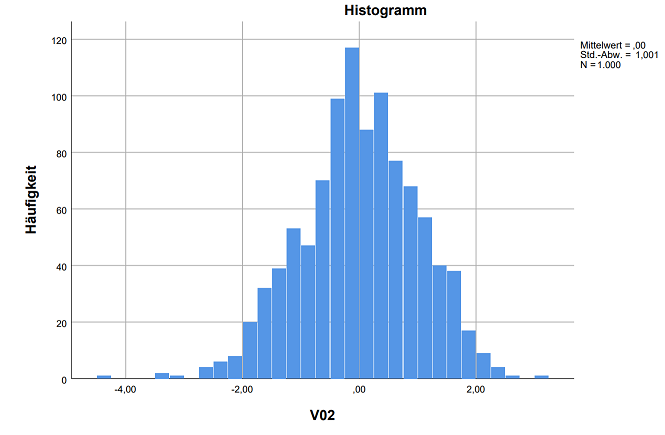
3.2 Q-Q-Diagramme
Die Q-Q-Diagramme bilden die erwarteten und die tatsächlichen Quantile ab. Die erwarteten Werte werden auf Basis der Normalverteilung gebildet. Sollten die tatsächlichen Werte jenen erwarteten (ungefähr) entsprechen, liegt eine Normalverteilung vor. Im Idealfall liegen alle Werte auf der Geraden, welche eine perfekte Normalverteilung abbildet. Hier sind die entsprechenden Q-Q-Diagramme für beide Variablen:
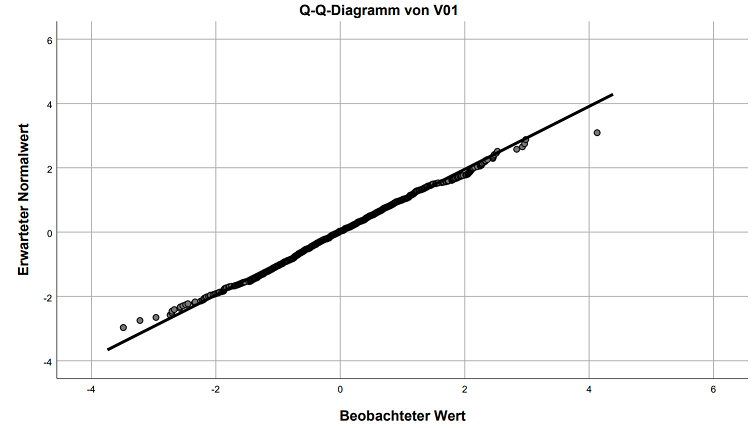
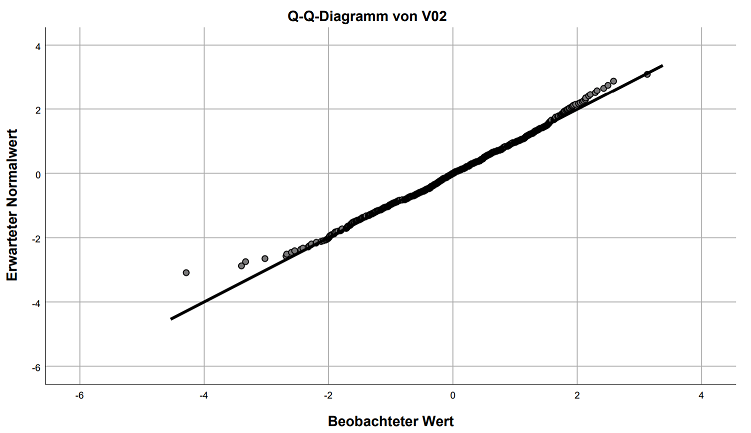
Man kann lediglich jeweils ganz links 3-4 Ausreißer erkennen und im ersten Diagramm ganz rechts. Insgesamt gibt es aber keinen Grund, allein deswegen eine Normalverteilung abzulehnen.
4 Zwei Beispielverteilungen – analytische Tests
Kommen wir nun zum eigentlichen Kern des Artikels: die analytischen Tests, Kolmogorov-Smirnov-Test und Shapiro-Wilk-Test und deren Ergebnisse. Ohne große Vorrede komme ich direkt zu den Resultaten. Eins noch. Die Nullhypothese geht von einer Normalverteilung der getesteten Variable aus, weshalb eine Signifikanz >0,05 erstrebenswert ist, um sie eben nicht ablehnen zu können.
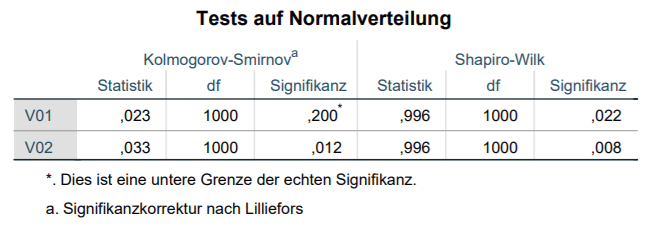
Wir erkennen bei den Ergebnissen nun folgendes. Für die Variable V01 hat der Kolmogorov-Smirnov-Test eine Signifikanz von 0,200 und behält damit die Nullhypothese von Normalverteilung bei. Der Shapiro-Wilk-Test hat allerdings für die Variable V01 eine Signifikanz von 0,022 und verwirft damit die Nullhypothese von Normalverteilung. Was stimmt denn nun? Erinnern wir uns an das Histogramm und Q-Q-Diagramm, liegt Normalverteilung mit sehr hoher Wahrscheinlichkeit vor. Wir erinnern uns auch, dass ich mir extra eine standardnormalverteilte Verteilung habe generieren lassen. Hier liegt also der Shapiro-Wilk-Test daneben. Zu dem Grund komme ich gleich, nachdem wir uns V02 angeschaut haben. Hier sagen sowohl Kolmogorov-Smirnov (p=0,012) als auch Shapiro-Wilk-Test (p=0,008), dass die Nullhypothese von Normalverteilung zu verwerfen ist. Aber woran liegt das, haben wir doch grafisch eine sehr gute Annäherung an eine perfekte Normalverteilung erhalten?
5 Das Problem großer Stichproben
Wir erinnern uns kurz, dass ich sagte, dass die Stichproben jeweils 1000 Fälle umfassen. Das ist auch das Problem. Die beiden (sowie alle anderen) analytischen Tests werden mit zunehmender Stichprobengröße sensibler für nur minimale Abweichungen von der Normalverteilung (Field (2018), S. 248-249). Das bedeutet, dass obwohl ich eine nahezu perfekte Normalverteilung habe, einige wenige Ausreißer reichen – meist sogar nur ein einziger – um die Signifikanz so sehr schrumpfen zu lassen, dass die Nullhypothese von Normalverteilung verworfen wird. Bei V01 ist es der Wert nahe 4, den man im Histogramm als auch im Q-Q-Diagramm sieht. Bei V02 ist es der Wert, der bei ca. -4,5 liegt. Nach deren Entfernung erhöhen sich die Signifikanzen jeweils leicht, ein paar andere Ausreißer wären aber noch zu entfernen. Alles in allem aber keine praktische Methode, wie ich hier etwas näher erläutere.
6 Das Fazit zu analytischen Tests bei großen Stichproben
Analytische Tests sind schön und gut, speziell Kolmogorov-Smirnov-Test und Shapiro-Wilk-Test. Sie drücken in einer Zahl – der Signifikanz – aus, was man wissen will: Normalverteilung liegt vor oder eben nicht. Man sollte sich als Anwender unbedingt dem oben beschriebenen Phänomen bewusst sein, dass minimale Abweichungen von einer nahezu perfekten Normalverteilung (zumindest unter praktischen Gesichtspunkten) bei immer größer werdenden Stichproben immer zu einer Ablehnung der Normalverteilung führt. Das kann im schlimmsten Falle zu einer falschen Entscheidung für ein nicht-parametrisches Verfahren führen. Das hat wiederum zur Folge, dass ihr eine (etwas) geringere Teststärke in Kauf nehmt und damit eine (etwas) geringere Chance habt, einen tatsächlich vorhandenen Effekt zu entdecken. Folglich empfehle ich wärmstens, die Tests eher kritisch zu betrachten und das Hauptaugenmerk auf Histogramm und Q-Q-Diagramm zu legen.
Abschließend sei auch darauf hingewiesen, dass generell mit sehr großen Stichproben die Chance bedeutungslose oder unwichtige Effekte (z.B. in Regressionen oder ANVOAs) aufzudecken steigt. Es sollte daher immer die Berechnung einer Effektstärke angeschlossen werden, um eine Quantifizierung der Relevanz des Effektes zu haben. In manchen Bereichen, wie z.B. der Medizin, würde ich es besonders kritisch sehen, in großen Stichproben nur auf den p-Wert zu schauen (vgl. beispielhaft Lantz (2013)).
7 Literatur
- Field, A. P. (2019). Discovering statistics using IBM SPSS statistics.
- Lantz, B. (2013), The large sample size fallacy. Scandinavian Journal of Caring Sciences, 27: 487-492. https://doi.org/10.1111/j.1471-6712.2012.01052.x
8 Das Video zum Beitrag


