Um latente Konstrukte zu erfassen, werden häufig Skalen verwendet. Diese setzen sich wiederum aus einer bestimmten Anzahl an Items (=Fragen) zusammen. Welche Möglichkeiten der Skalenbildung durch Items existieren, zeigt dieser Artikel.
Inhaltsverzeichnis
1 Ausgangssituation – eine Skala und sie bildende Items
Am sinnvollsten ist das Verwenden bereits existierender Skalen für latente Konstrukte. Dies spart die aufwändige Prüfung der Validität (aber nicht Reliabilität). Diese Skalen findet man in Skalenhandbüchern der jeweiligen Fachdisziplin oder z.B. bei Institutionen wie der GESIS. Zumeist wird neben den expliziten Formulierungen der Fragen auch eine Empfehlung über die Skalierung und den Wertebereich der einzelnen Items gegeben, inklusive möglicher Kontrollfragen. Ich verwende die sog. “Happiness and Satisfaction Scale“, die über lediglich drei Items gemessen wird:
- Happiness in general (If you were to consider your life in general, how happy or unhappy would you say you are, on the whole?)
- Satisfaction with job (All things considered, how satisfied are you with your (main) job?)
- Satisfaction with family life
Die Beantwortung erfolgt über eine 7-stufige Likert-Skala, die für das 1. Item von 1 (completely happy) bis 7 (completely unhappy) und für das 2. und 3. Item ebenfalls von 1 (completely satisfied) bis 7 (completely dissatisfied) reicht. Eine Umkodierung ist für sie notwendig und zeige ich in diesem Beitrag.
2 Codierung der Items prüfen
Kontrollfragen sollen verhindern, dass Befragte den Fragebogen einfach unüberlegt durchkreuzen bzw. dass ein solches Verhalten dem Datenerhebenden auffällt. Bevor eine Zusammenfassung von Items zu einer Skala vorgenommen wird, sollte daher in der Dokumentation zur Skala geprüft werden, welche Kontrollfragen existieren und ob diese umzukodieren sind. Wie, zeigt der Artikel zum Umcodieren von inversen Items.
3 Skala bilden – der Mittelwert
Das Bilden eines Mittelwertes funktioniert über den Menüpunkt “Transformieren -> Variable berechnen”. Hier kann man prinzipiell die Funktion MEAN verwenden – dies sollte man aber nur tun, wenn keine fehlenden Werte existieren. Die einzelnen Items der Skala werden mit Komma getrennt in den Ausdruck MEAN() gesetzt. Eine Zielvariable wird ebenfalls definiert, in meinem Fall “Happiniess_Mean”. In dieser steht nun für jeden Fall der Mittelwert der 3 Items “Happy_general”, “Satisfaction_family” und “Satisfaction_job”.
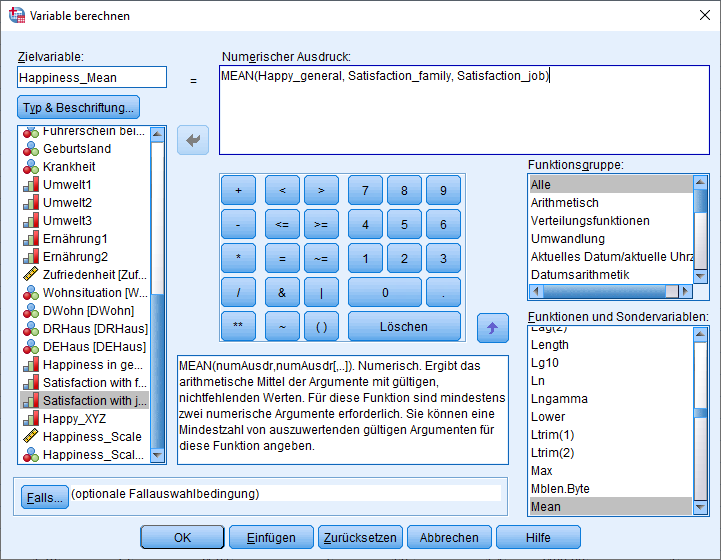
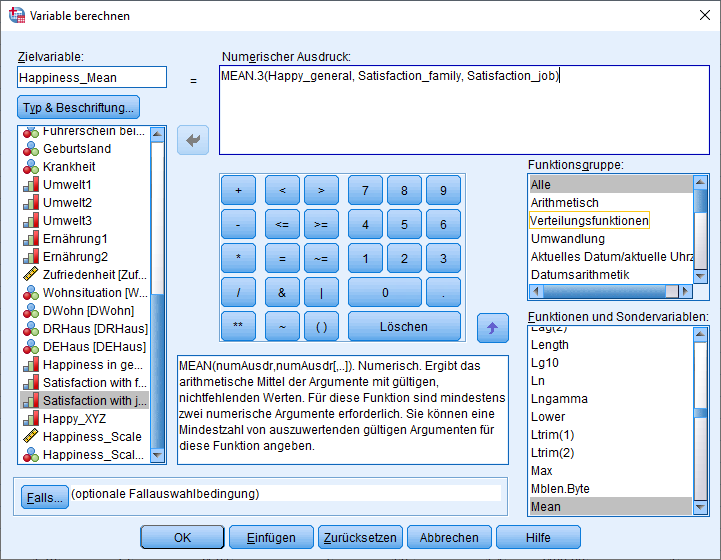
Existieren fehlende Werte bei den Items, sollte allerdings nicht mit der MEAN-Funktion gearbeitet werden. Hier empfiehlt sich die MEAN.X-Funktion. X ist hierbei die Anzahl an Variablen, die nicht fehlend sein darf. Wenn ich im Beispiel MEAN.3 () verwende, müssen alle drei Items vorhanden sein, damit ein Mittelwert berechnet wird. Fehlt nur 1 Item, wird der Mittelwert nicht berechnet und der Proband bekommt keinen “Happiness_Mean”-Score und fällt somit als fehlend in den Folgeanalysen heraus.
In SPSS sieht das so aus:
4 Skala bilden – der Summenscore
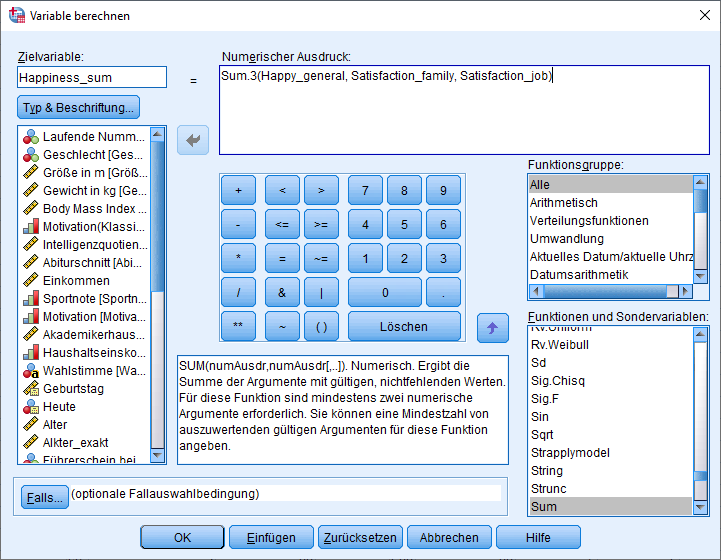
Das Prinzip der Berechnung sollte nun bereits hinreichend deutlich geworden sein. Die Berechnung des Summenscore funktioniert mit der Funktion SUM bzw. SUM.X analog zu der Mittelwertfunktion. Ich habe hier direkt die SUM.3-Funktion berechnen lassen und mir in der Variable “Happiness_sum” speichern lassen.
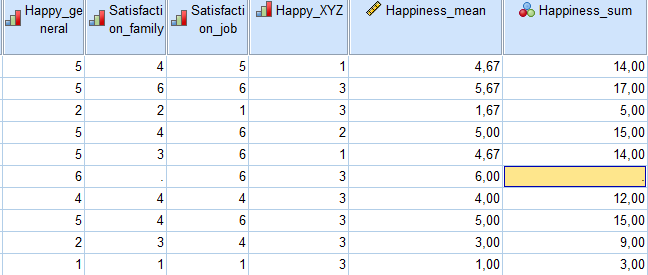
Im Ergebnis sieht das so aus, dass ein Fall mit fehlenden Werten dann auch direkt einen fehlenden Wert bei der Skalenbildung bekommt. Hinweis: bei “Happiness_mean” wurde nicht mit MEAN.X gearbeitet, weswegen dort ein Wert von 6 steht, “Happiness_sum” aber fehlend ist.
5 Hinweise zum Schluss
- Gerade bei einem Summenscore ist es sehr wichtig auf fehlende Werte zu prüfen. Wenn im obigen Fall die Summe aus 6, fehlend und 6 gebildet wird, wäre das 12 und ein durchaus plausibler Wert. Allerdings hätte der Proband mit hoher Wahrscheinlichkeit beim fehlenden Wert einen von 0 bzw. dem Itemminimum von 1 verschiedenen Wert und eine Summe größer 12. Man würde dem Proband demzufolge eine geringere Zufriedenheit attestieren – aber nur aufgrund fehlender Daten. Daher mein Appell, besonders beim Summenscore mit SUM.X zu arbeiten.
- Beim Mittelwert ist es meist nicht ganz so dramatisch, wenn ein Item fehlt, allerdings sollte auch hier besser mit der MEAN.X-Funktion gearbeitet werden, um potenzielle Verzerrungen zu vermeiden. Es ist nur ein .X mehr in der Funktion zu tippen und erspart einem hinterher mitunter viel Interpretationsaufwand. 😉


