Inhaltsverzeichnis
1 Was ist Heteroskedastizität?
Heteroskedastizität ist im Kontext der einfachen linearen Regression oder multiplen linearen Regression eine zunehmende oder abnehmende Streuung der Residuen (mitunter auch Fehlerterme genannt). Die Residuen müssen allerdings homoskedastisch sein, also eine gleichmäßige lineare Streuung in allen Bereichen aufweisen.
2 Was hat Heteroskedastizität für Folgen?
Die Standardfehler der Regressionskoeffizienten werden bei vorhandener Heteroskedastizität (nach oben) verzerrt geschätzt. Sie sind damit nicht konsistent. Das führt wiederum dazu, dass die t-Werte nicht verlässlich geschätzt werden können. Schließlich führt das zu verzerrten p-Werten und damit zu einer Gefahr einer falschen Hypothesenentscheidung: insbesondere eine fälschliche Annahme der Nullhypothese (Fehler 2. Art) ist häufig die Folge. Achtung: die Koeffizienten selbst sind im Rahmen der Regression nicht verzerrt.
3 Grafisches Erkennen von Heteroskedastizität in SPSS
Die (meiner Meinung nach) einfachste und schnellste Möglichkeit bei einer Regression in SPSS auf Heteroskedastizität zu prüfen, ist die grafische (Anleitung für die analytische Prüfung in diesem Artikel). Hierzu lässt man sich ein Streudiagramm ausgeben, das die standardisierten vorhergesagten Werte und die standardisierten Residuen enthält. Dazu geht man über “Analysieren” -> “Regression”. Zunächst ist das Regressionsmodell wie gewohnt zu spezifizieren. In meinem Falle ist die abhängige Variable der Abiturschnitt, die unabhängigen Variablen sind der Intelligenzquotient und die Motivation. Als Nächstes ist die Schaltfläche “Diagramme” zu wählen, wo sich folgendes Dialogfeld öffnet:
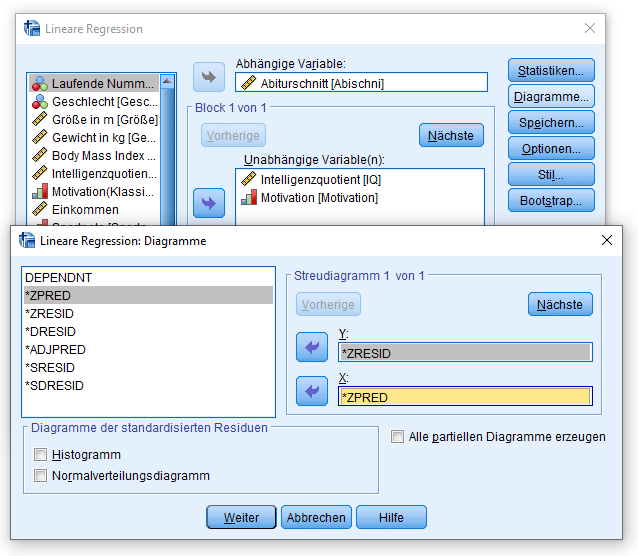
SPSS bezeichnet die standardisierten vorhergesagten Werte als *ZPRED und die standardisierten Residuen als *ZRESID. *ZPRED kommt in die x-Box, *ZRESID kommt in die y-Box. Nach einem Klick auf Weiter und der Berechnung der Regression erhält man den kompletten SPSS-Output. Für Heteroskedastizität ist allerdings lediglich das Diagramm mit standardisierten vorhergesagten Werte und standardisierten Residuen interessant:
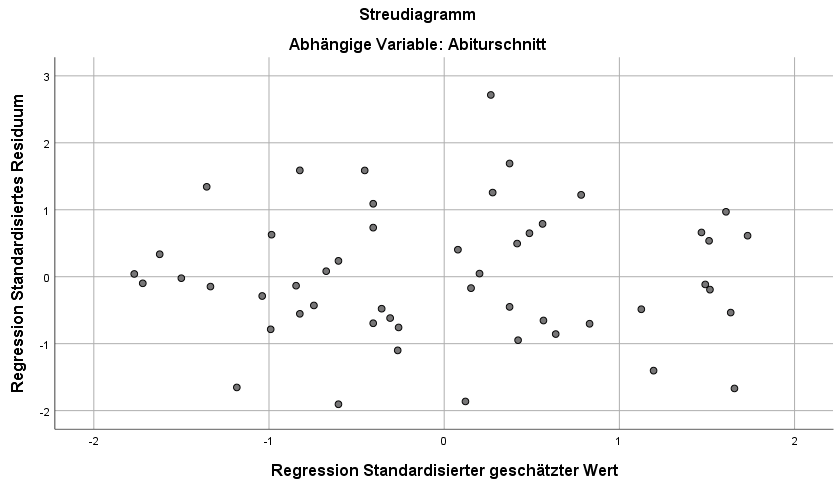
Da im obigen Diagramm keine Zunahme oder Abnahme der Streuung erkennbar ist, also man keinen nach links oder rechts geöffneten Trichter erkennen kann, würde man hier keine Heteroskedastizität unterstellen.
4 Was tun bei Heteroskedastizität?
Es gibt verschiedene Wege Heteroskedastizität zu kontern. Es besteht die Möglichkeit, eine Weighted Least Squares Regression zu rechnen. Allerdings ist das unnötig kompliziert und auch im Hinblick auf die Interpretation. Viel einfacher und direkt in SPSS implementiert ist die Verwendung von heteroskedastizitätskonsistenten bzw. heteroskedastizitätsrobusten Schätzern. Dies hat zur Folge, dass die Standardfehler nicht mehr verzerrt sind.
Diese Funktion ist allerdings nicht im Regressions-Dialogfeld implementiert. Dazu muss man über “Analysieren -> Allgemeines lineares Modell ” -> “Univariat” gehen.
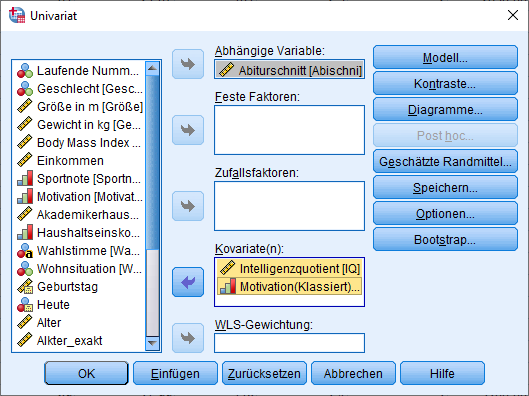
Als abhängige Variable wird logischerweise eure abhängige Variable eingetragen. Eure unabhängigen Variablen kommen in die Box “Kovariate(n)“. Als Nächstes geht ihr auf die Schaltfläche Optionen und erhaltet Folgendes:
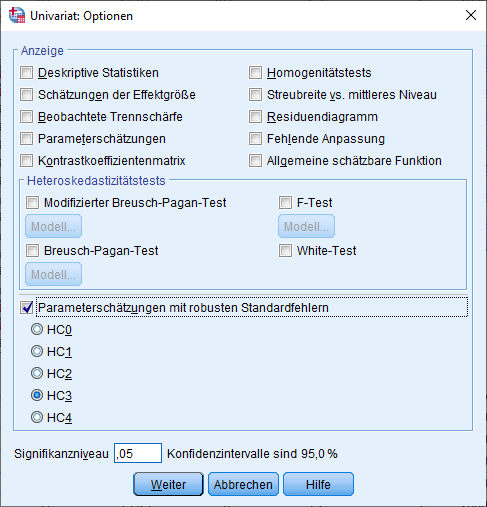
Euch interessiert an dieser Stelle lediglich “Parameterschätzungen mit robusten Standardfehlern“. Hier setzt ihr einen Haken und könnt nun zwischen HC0, HC1, HC2, HC3 und HC4 auswählen. Welcher robuste Standardfehler ist der “beste”? Es gibt keinen besten, aber einige Richtlinien von Hayes (2007), S. 713:
- Cribari-Neto (2005) simulation results also suggest the superiority of HC3 over its predecessors (HC0-HC2).
- Cribari-Neto’s (2004) simulations show that HC4 can outperform HC3 in terms of test size control when there are high leverage points and nonnormal errors.
Laut Hayes empfiehlt sich am ehesten HC3. HC4 ist dann sinnvoll, wenn die Residuen nicht normalverteilt sind oder high leverage points existieren. Letzere sind Ausreißer, die – grafisch gesprochen – insbesondere in x-Richtung auftreten
Nach der Ausführung von HC3 erhaltet ihr eine Tabelle “Parameterschätzungen mit robusten Standardfehlern“, die ihr dann wie gewohnt zur Interpretation eurer Regression verwenden könnt. In diesem Artikel gibt es noch ein paar zusätzliche Zeilen dazu.
Hinweis: Es gibt inzwischen auch HC5, dieser ist allerdings noch nicht in SPSS implementiert. In früheren Versionen von SPSS (24 oder niedriger) ist keine Schätzung von robusten Standardfehlern implementiert.
5 Literatur
Hayes, A. F., & Cai, L. (2007): Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation. Behavior research methods, 39(4), 709-722


