Inhaltsverzeichnis
1 Was ist Heteroskedastizität?
Heteroskedastizität ist im Rahmen der einfachen linearen Regression oder multiplen linearen Regression eine zunehmende oder abnehmende Streuung der Residuen (mitunter auch Fehlerterme genannt). Die Residuen müssen allerdings homoskedastisch sein, also eine gleichmäßige lineare Streuung in allen Bereichen aufweisen.
2 Was hat Heteroskedastizität für Folgen?
Die Standardfehler der Regressionskoeffizienten werden bei vorhandener Heteroskedastizität (nach oben) verzerrt geschätzt. Sie sind damit nicht konsistent. Das führt wiederum dazu, dass die t-Werte nicht verlässlich geschätzt werden können. Schließlich führt das zu verzerrten p-Werten und damit zu einer Gefahr einer falschen Hypothesenentscheidung: insbesondere eine fälschliche Annahme der Nullhypothese (Fehler 2. Art) ist häufig die Folge. Achtung: die Koeffizienten selbst sind im Rahmen der Regression nicht verzerrt.
3 Erkennen von Heteroskedastizität in R
3.1 Grafische Erkennung von Heteroskedastizität
Die (meiner Meinung nach) einfachste und schnellste Möglichkeit bei einer Regression in R auf Heteroskedastizität zu prüfen, ist die grafische. Hierzu lässt man sich ein Streudiagramm ausgeben, das die vorhergesagten Werte und die Residuen enthält. Wahlweise können diese auch standardisiert sein.
In R muss dazu das Modell zunächst berechnet werden, was wie folgt, in meinem Beispiel lauten könnte:
model <- lm(Abischni~IQ+Motivation, data = data_xls)
Wichtig ist hier, sich den Modellnamen zu merken. In meinem Fall heißt es schlicht "model".
Als Nächstes braucht es schon den Code für die Ploterstellung. Hierzu existieren 2 Möglichkeiten, beide nutzen die plot()-Funktion.
#1
plot(model, 1)
#2
plot(fitted.values(model), rstandard(model))
Hieraus erhält man zwei Diagramme, die grundsätzlich dasselbe darstellen:
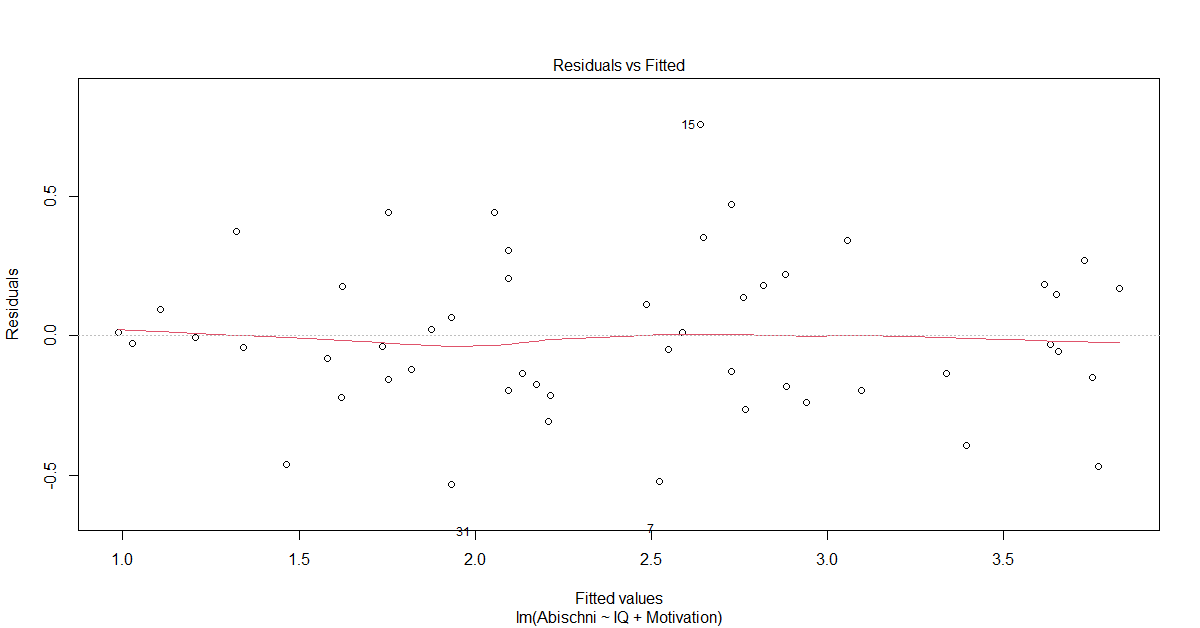
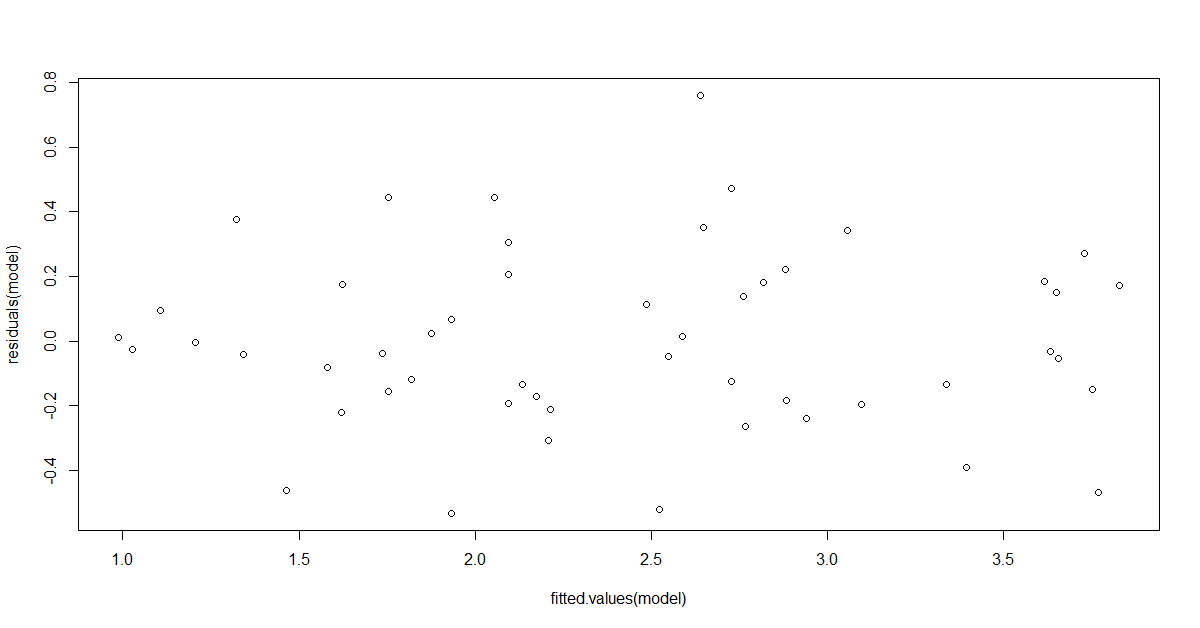
Zunächst schaut man sich nur die Streuung der Punkte an. Da im obigen Diagramm keine Zunahme oder Abnahme der Streuung erkennbar ist, also man keinen nach links oder rechts geöffneten Trichter erkennen kann, würde man hier zunächst eher keine Heteroskedastizität unterstellen.
Das obere Diagramm hilft zusätzlich mit einer roten Linie, die möglichst gerade sein sollte. Ist sie wellig oder hat eine positive oder negative Steigung, würde man definitiv von Heteroskedastizität sprechen. Wie wir noch sehen werden, kommen wir mit der folgenden analytischen Prüfung auf ein anderes Ergebnis. Diesen Konflikt kann man aber auch recht einfach auflösen - pauschal robuste Standardfehler schätzen lassen - mehr im Abschnitt "Was tun bei Heteroskedastizität".
3.2 Analytische Erkennung von Heteroskedastizität
Hierzu verwendet man entweder den White-Test oder den Breusch-Pagan-Test. Ersterer wird häufiger bei leichten Verletzungen der Normalverteilungsannahme eingesetzt. Diesen findet man im Paket "lmtest", welches über install.packages() installiert und über library() geladen werden kann. In die Funktion bptest() fügt man den Modellnamen ein. Im Beispiel ist es erneut "model".
install.packages("lmtest")
library(lmtest)
bptest(model)
Der Output ist recht kurz gehalten. Der Breusch-Pagan-Test prüft die Nullhypothese von Homoskedastizität. Ein geringer p-Wert verwirft diese und nimmt die Alternativhypothese von Heteroskedastizität an.
studentized Breusch-Pagan test
data: model
BP = 8.3438, df = 2, p-value = 0.01542
Tatsächlich verwirft der Breusch-Pagan-Test für mein Modell die Nullhypothese von Homoskedastizität mit dem p-Wert von 0,01542. Demzufolge ist die Alternativhypothese von Heteroskedastizität der Residuen anzunehmen.
ACHTUNG: Analytische Tests verwerfen die Nullhypothese mit zunehmender Stichprobengröße häufiger, obwohl die Abweichungen marginal sind. Deswegen ist die grafische Methode (mit roter Linie) häufig die bessere Wahl bei mehreren hundert Beobachtungen. Bei kleineren Stichproben gilt der Test jedoch als hinreichend zuverlässig.
4 Was tun bei Heteroskedastizität?
Es gibt verschiedene Wege Heteroskedastizität zu kontern. Es besteht die Möglichkeit, eine Weighted Least Squares Regression zu rechnen. Allerdings ist das unnötig kompliziert, auch im Hinblick auf die noch vorzunehmende Interpretation. Viel einfacher und über das "lmtest"-Paket in R implementiert ist die Verwendung von heteroskedastizitätskonsistenten bzw. heteroskedastizitätsrobusten Schätzern. Dies hat zur Folge, dass die Standardfehler nicht mehr verzerrt sind und damit auch nicht die t-Werte und p-Werte.
Diese Funktion wird wieder über install.packages() und library() installiert und geladen. Danach führt man die coeftest()-Funktion aus, gibt allerdings noch den Befehl vcov() hinzu, der die Berechnung von heteroscedasticity consistent (HC) standard errors ermöglicht. Es gibt beim type verschiedene, nämlich "HC", "HC0", "HC1", "HC2", "HC3", "HC4", "HC4m", "HC5" Schätzmöglichkeiten.
Welcher robuste Standardfehler ist der "beste"? Es gibt keinen besten, aber einige Richtlinien von Hayes (2007), S. 713:
- Cribari-Neto (2005) simulation results also suggest the superiority of HC3 over its predecessors (HC0-HC2).
- Cribari-Neto’s (2004) simulations show that HC4 can outperform HC3 in terms of test size control when there are high leverage points and nonnormal errors.
Laut Hayes empfiehlt sich am ehesten HC3. HC4 ist dann sinnvoll, wenn die Residuen nicht normalverteilt sind oder high leverage points existieren. Letztere sind Ausreißer, die - grafisch gesprochen - insbesondere in x-Richtung auftreten
install.packages("lmtest")
library(sandwich)
coeftest(model, vcov = vcovHC(model, type = "HC3"))
Nach der Ausführung von HC3 erhaltet ihr eine neue Koeffiziententabelle.
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.5580099 0.5790595 13.0522 < 2.2e-16 ***
IQ -0.0392151 0.0068176 -5.7521 5.983e-07 ***
Motivation -0.1393233 0.0356805 -3.9047 0.0002943 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Wenn ihr die Tabelle mit dem normalen Output der Regression vergleicht, werdet ihr feststellen, dass sich die Koeffizienten ("Estimates") nicht verändert haben, wohl aber alles, was rechts davon steht, also Standardfehler (Std. Error), t-Werte und p-Werte.
Hier zum Vergleich die Ausgangswerte des Modells
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.558010 0.397176 19.029 < 2e-16 ***
IQ -0.039215 0.004477 -8.759 1.61e-11 ***
Motivation -0.139323 0.024350 -5.722 6.66e-07 ***
Es ist erkennbar, dass die p-Werte der Koeffizienten im Ausgangsmodell deutlich über denen nach der Schätzung mit HC3 liegen. Demzufolge hat das Modell aufgrund Heteroskedastizität die Standardfehler als zu niedrig und damit in letzter Instanz die p-Werte als zu niedrig eingeschätzt. Fehler 1. Art können hier also tatsächlich auftreten, wenn die p-Werte näher an der Verwerfungsgrenze liegen.
Zur besseren Übersicht hier noch mal eine kleine Tabelle.
rob. rob.
Koeffizient Standardfehler Standardfehler p-Wert p-Wert
IQ 0.004477 0.0068176 1.61e-11 5.98e-07
Motivation 0.024350 0.0356805 6.66e-07 0.000294
5 Literatur
Hayes, A. F., & Cai, L. (2007): Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation. Behavior research methods, 39(4), 709-722


