Konzentrationsmaße sollen einen Überblick über die Konzentration eines z. B. bestimmten Marktes geben. Das Erkenntnisziel ist also, ob ein Markt z.B. oligopolistisch oder gar monopolistisch geprägt ist. Ein Maß für Konzentration ist der Herfindahl-Hirschman-Index, bisweilen auch nur Herfindahl-Index.
Inhaltsverzeichnis
1 Den Herfindahl-Index in Excel berechnen
![Rendered by QuickLaTeX.com \[ HHI=\sum_{i=1}^{N}{{\frac {q_{i}}{\sum _{j=1}^{N}{q_{j}}}}}}\]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-f1f8aa9958171f79a39accd0d0acf1e3_l3.png)
Hierzu braucht es nicht viel Vorbereitung. Es braucht nicht mal eine sortierte Urliste. Ihr braucht lediglich das zu untersuchende Merkmal. Im Beispiel habe ich die Marktwerte (in Mio. Euro) der Bundesligaclubs aus einer vergangenen Saison bereits aufsteigend sortiert, also vom geringsten zum höchsten Wert. Da der HHI die relativen Marktanteile der Unternehmen quadriert, aufsummiert, sind zunächst noch zwei Zwischenschritte erforderlich.
1.1 Die relativen Marktanteile berechnen
Um die relativen Marktanteile zu berechnen, benötigt man die Gesamtsumme der Marktwerte. Hierzu kann man einfach die Summen-Funktion von Excel verwenden. Mit “=SUMME(C2:C19)” erhalte ich eine Gesamtsumme der Marktwerte von 2666,03 Mio. Euro, die in der Zelle C20 stehen.
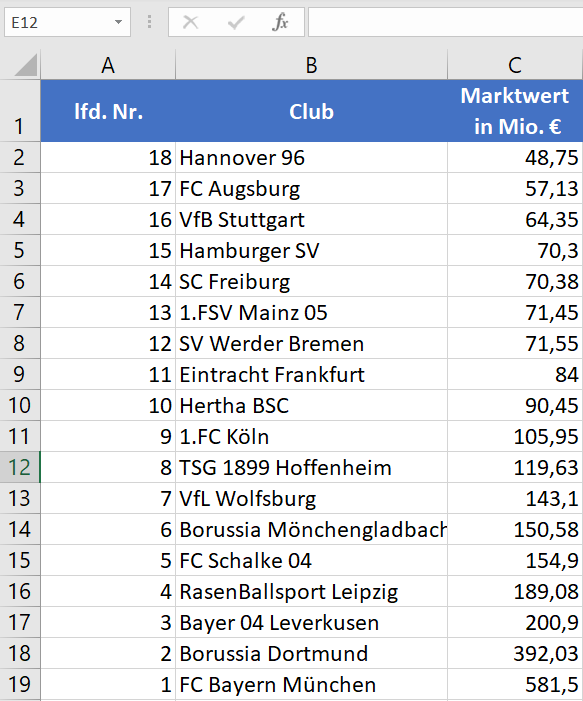
Jetzt muss ich nur noch lediglich den Marktwert jedes Clubs durch die Gesamtsumme der Marktwerte teilen. Am Beispiel des VfB Stuttgart erkennt man 64,35 Mio. Euro (Zelle C4) von 2666,03 Mio. Euro (Zelle C20) sind stolze 0,0241 (Zelle D4), also 2,4% der Gesamtsumme der Marktwerte. Borussia Dortmund hingegen kommt auf 14,7%. Am einfachsten ist die relative Berechnung, indem in der Formel statt mit “=C4/C20” die Gesamtsumme der Marktwerte mit markieren von C20 innerhalb der Formel und Fixierung dessen (Taste F4) erfolgt: “=C4/$C$20”. Dann kann anschließend mit der Autofüll-Funktion gearbeitet werden.

1.2 Die relativen Marktanteile quadrieren
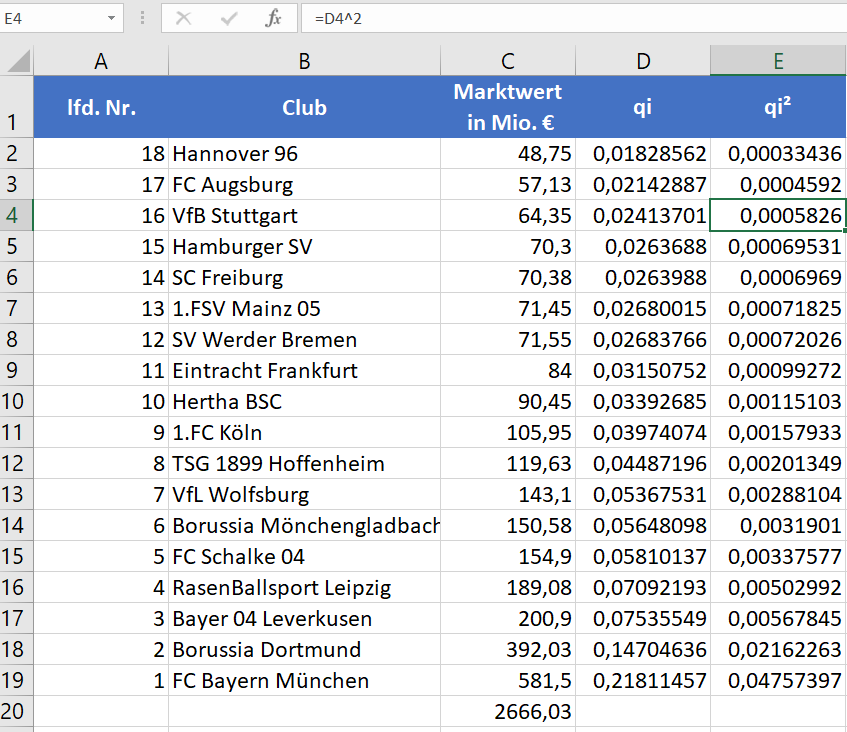
Wie an der HHI-Formel erkennbar ist, sind diese Marktanteile jetzt lediglich zu quadrieren. Hierzu wird in der Spalte D der Werte von Spalte C lediglich quadriert. Hierzu kann man in Zelle E4 also einfach schreiben “=D4^2”.
1.3 Die Gesamtsumme der quadrierten Marktanteile berechnen
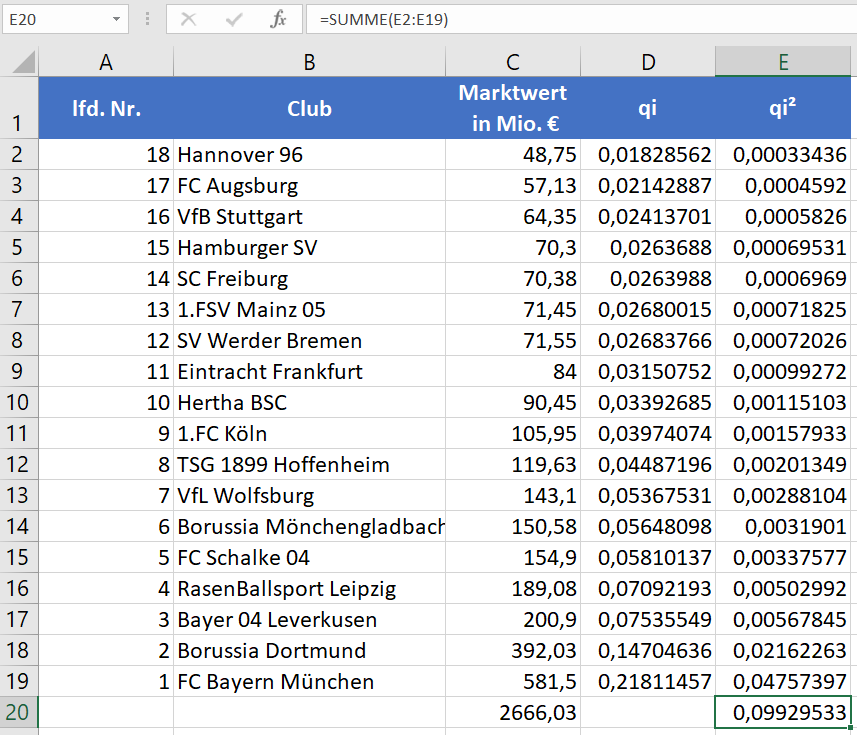
Zum Schluss ist lediglich über die quadrierten Marktanteile die Summe zu berechnen. Hierzu verwendet man erneut die Summenfunktion “=SUMME(E2:E19)”. Im Beispiel ist dieser Wert gerundet 0,0993.
2 Den Herfindahl-Index interpretieren
Der HHI hat einen Wertebereich von 1/N bis 1. Er kann für 18 Bundesligaclubs demnach im niedrigsten Fall 1/18 = 0,056 sein.
Dennoch gibt es verschiedene Stufen, zur Interpretation des Herfindahl-Index. Sie sind wie folgt:
- < 0,15: unkonzentrierter Markt
- 0,15 – 0,25: moderat konzentrierter Markt
- > 0,25: hoch konzentrierter Markt
Naldi, M., & Flamini, M. (2014). The CR4 index and the interval estimation of the Herfindahl-Hirschman Index: an empirical comparison.
Im Beispiel würde man einem Wert von gerundet 0,0993 also einen eher unkonzentrierten Markt unterstellen. Fakt ist, dass im unteren Bereich eine sehr geringe Konzentration beobachtbar ist. Alle Clubs zwischen Hannover 96 (niedrigster Marktwert) und Schalke 04 (fünfthöchster Marktwert) haben einen relativen Marktanteil zwischen 1,8% und 5,8%. Ab RB Leipzig steigen die relativen Marktanteile dann aber schon recht stark. Die 4 marktwertstärksten Clubs vereinen knapp 50% auf sich, was nicht wenig ist. Von daher kann man vorsichtig schließen, dass gerade mit Bayern München und Borussia Dortmund zwei sehr wertvolle Clubs die Liga dominieren, danach ist es aber ein nur sehr leichtes Gefälle, bezogen auf den Marktwert.
3 Der normierte/standardisierte Herfindahl-Index
Der normierte bzw. standardisierte Herfindahl-Index (HHI*) hat den Vorteil, dass er für die Anzahl an Unternehmen kontrolliert, was sich auf dern Wertebereich auswirkt. Der Wertebereich beim HHI* ist 0 bis 1, also unabhängig der Anzahl der Unternehmen interpretierbar. Er berechnet sich wie folgt:
![]()
Im Beispiel wäre dies:
![]()


