Friedman-Test in SPSS rechnen

1 Ziel des Friedman-Test in SPSS

Der Friedman-Test ist ein nicht parametrischer Mittelwertvergleich bei 3 oder mehr abhängigen Stichproben. Der Friedman-Test verwendet allerdings (mittlere) Ränge statt die tatsächlichen Werte und ist das Gegenstück zur ANOVA mit Messwiederholung. Sein Vorteil ist, das er quasi keine Voraussetzungen hat.

2 Voraussetzungen des Friedman-Tests in SPSS

• mindestens drei voneinander abhängige Stichproben/Gruppen
• ordinal oder metrisch skalierte y-Variable
• normalverteilte y-Variable innerhalb der Gruppen nicht nötig

3 Durchführung des Friedman-Tests in SPSS

Über das Menü in SPSS: Analysieren > Nichtparametrische Test > Verbundene Stichproben

Unter dem Reiter Variablen sind die Testvariablen zu definieren. Als Variablen sind die zu testenden, also die abhängigen Variablen einzusetzen. Typischerweise hat man zu jedem Zeitpunkt eine Messung für alle Individuen vorliegen. In meinem Falle heißen die Variablen wie die Zeitpunkte: T1, T2 und T3.

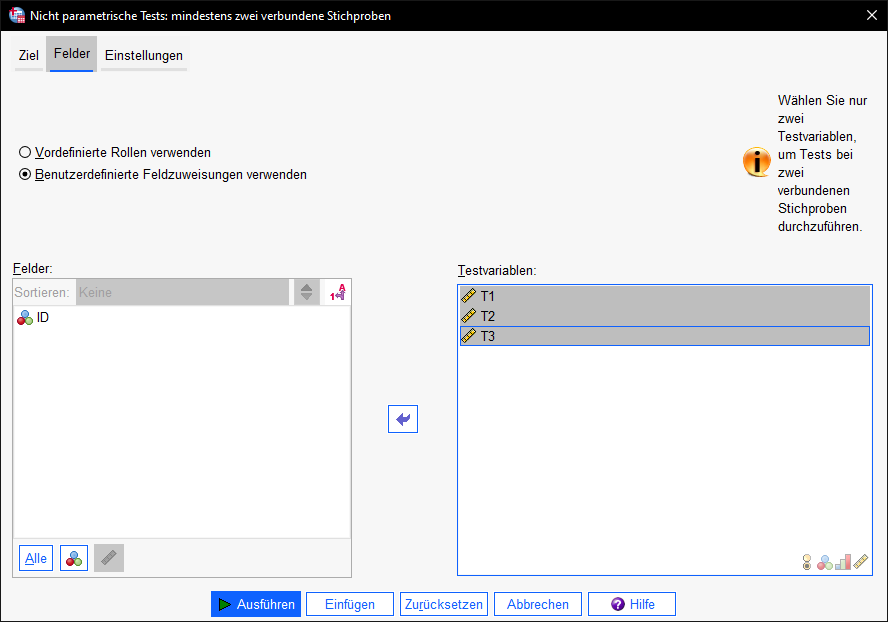
Als Test muss unter dem Reiter Einstellungen der Friedman-Test ausgewählt werden. Dazu wählt ihr 1) “Tests anpassen” und bei “Verteilungen vergleichen” ist 2) “Friedmans zweifaktorielle ANOVA nach Rang” auszuwählen. Bei Mehrfachvergleiche empfiehlt sich zudem “Alle paarweise” auszuwählen”.

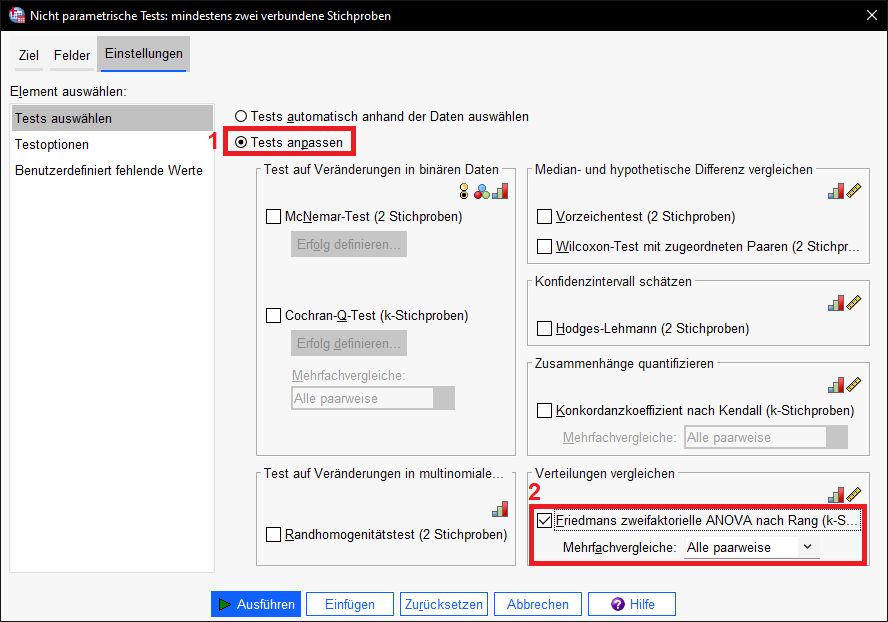
Ein Klick auf “Ausführen” führt die Berechnung durch und zeigt die Ergebnisse an.

4 Interpretation der Ergebnisse des Friedman-Tests in SPSS

Die Hypothesenübersicht gibt zunächst lediglich an, was mit der Nullhypothese (Gleichheit der mittleren Ränge) zu geschehen hat. Aufgrund dessen, dass die Signifikanz in meinem Beispiel mit p < .001 hinreichend klein ist (unter dem typischen Alphawert von 0,05), ist die Nullhypothese entsprechend abzulehnen. Dies wird von SPSS auch angezeigt, wenn es der in einer Berechnung der Fall ist. Sollte dies nicht der Fall sein, gibt auch SPSS hierüber Auskunft.

Darunter gibt es ein um 90 Grad gedrehtes Histogramm pro Zeitpunkt, welches die Häufigkeiten pro Ausprägung sowie die mittleren Ränge.

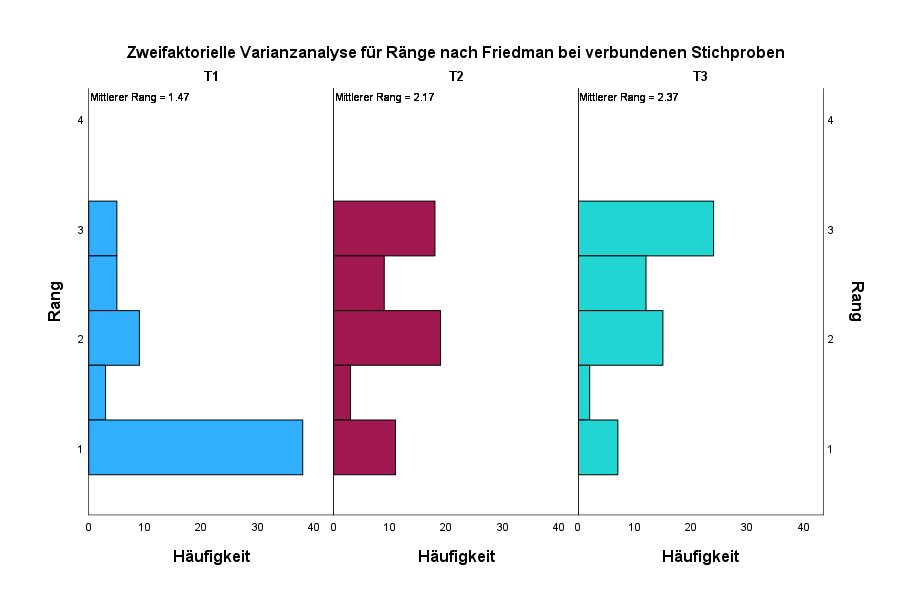
Hieran schließt sich noch die Testzusammenfassung an, die beim Berichten noch wichtig wird. Sie zeigt dasselbe Ergebnis wie die Hypothesenübersicht von oben: an der sehr kleinen Signifikanz von p < .001. ist ein Unterschied ablesbar

Allerdings erkennt man hieraus nicht, ob zwischen den Zeitpunkt T1 und T2, T2 und T3 oder T1 und T3 ein Unterschied besteht. Dies erkennt man erst, wenn man die angeforderten paarweisen Vergleiche (post-hoc-Tests) betrachtet.

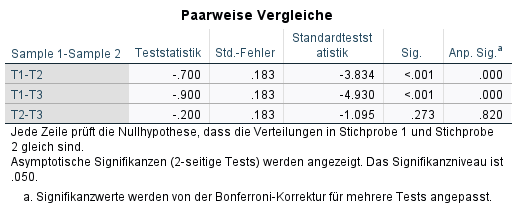
Die dann angezeigte Tabelle zeigt für alle paarweisen Vergleiche (hier die eben genannten drei) in der letzten Spalte die Angepassten Signifikanzen, die zur Beurteilung herangezogen werden.
Die Signifikanz ist deswegen angepasst, weil hier für die Mehrfachtestung auf dieselbe Stichprobe kontrolliert wird. Das dient zur Vermeidung von Alphafehlerkumulierung (hohe Wahrscheinlichkeit, die Nullhypothese fälschlicherweise abzulehnen). Es wird die normale Signifikanz mit der Anzahl der Tests multipliziert. Bei T2-T3 sieht man dies ganz gut. Die normale Signifikanz ist p = 0.273. Es sind 3 paarweise Vergleiche, somit ist 0.273*3 = 0.820

Im Fall des Beispiels sind die Unterschiede zwischen T1 und T2 sowie T1 und T3 beobachtbar, da die angepassten Signifikanzen mit p < .001 hinreichend klein sind. Der Unterschied zwischen T2 und T3 hat keinen hinreichend kleinen p-Wert. Die Intervention nach T1 scheint also direkt gewirkt zu haben, und zumindest in der direkten Folgemessung konstant zu bleiben.

5 Ermittlung der Effektstärke des Friedman-Tests

Die Effektstärke des Friedman-Tests selbst wird mit Kendall’s ω bzw. meist Kendall’s W angegeben. Dieses kann über zwei Wege berechnet werden.
1) Mit folgender Formel aus Schapiro Grosof, M., Sardy, H. (2014):

Die Werte können aus der Testzusammenfassungstabelle entnommen werden. X² ist die Teststatistik, N die Anzahl der Beobachtungen und K die Anzahl der Zeitpunkte.

2) Über SPSS: Analysieren > Nichtparametrische Tests > Klassische Dialogfelder > K verbundene Stichproben

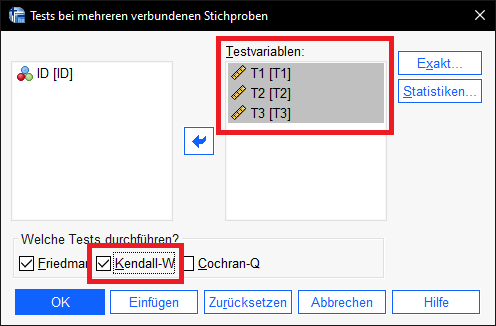
Die Messwerte zu den Zeitpunkten werden entsprechend in das Feld Testvariablen geschoben.
Bei der Frage nach der Auswahl der Tests ist Kendall-W auszuwählen.

Im Ergebnis erhält man eine kleine Übersicht, die denselben Wert für Kendall’s W wie oben berechnet ausgibt:

W = 0.240 ist noch einzuordnen. Idealerweise existieren vergleichbare Studien oder fachspezifische Grenzen. Wenn nicht, kann Cohen (1992) S. 157 herangezogen werden. Die Grenzen sind 0.1, 0.3 und 0.5 für kleine, mittlere und große Effekte.

HINWEIS: Zumeist ist Kendall’s W für andere Forscher hilfreich, die eine Studie planen, um Anhaltspunkte für die Mindeststichprobenberechnung zu haben. Die nachfolgend berechneten Effektstärken für die paarweisen Vergleiche haben einen größere Bedeutung in der Quantifizierung von Unterschieden über die Zeit.

6 Ermittlung der Effektstärken der post-hoc-Tests

Viel erkenntnisreicher ist die Berechnung der Effektstärke für die paarweisen Vergleiche, weil damit erkannt werden kann, wie groß die Unterscheide im Zeitablauf sind. Hierzu bedarf es lediglich der standardisierten Teststatistik z und der Anzahl der Beobachtungen (n)

Die Effektstärke r wird mit folgender Formel berechnet. Der z-Wert (Standardteststatistik aus der Tabelle paarweise Vergleiche) wird durch die Wurzel der Stichprobengröße geteilt. Aufgrund der Betragsstriche wird dieser Quotient immer positiv sein.

• Im Beispiel ist also für T1-T2 der z-Wert -3.834 durch die Wurzel aus 60 zu teilen und der Betrag dessen zu nehmen. Das Ergebnis hieraus lautet: 0.495.

     

• Für T1-T3:

     

Zur Einordnung der Effektstärken werden vergleichbare Studien herangezogen oder fachspezifische Grenzen genutzt. Existiert beides nicht können die Grenzen von Cohen: Statistical Power Analysis for the Behavioral Sciences (1988), S. 79-81 verwendet werden.

• ab 0,1 ist es ein schwacher Effekt
• ab 0,3 ist es ein mittlerer Effekt
• und ab 0,5 ist es ein starker Effekt.

Im vorliegenden Beispiel sind, nach Cohen (1988), die Effektstärken knapp unter der Grenzen zum starken Effekt (T1-T2) bzw. über der Grenze zum starken Effekt (T1-T3).

7 Reporting

Beim Reporting wird zunächst der Friedman-Test samt Teststatistik, Freiheitsgrade und p-Wert berichtet. Anschließend werden die paarweisen Vergleiche, die hinreichend kleine p-Werte aufweisen angegeben, behelfsweise auch deren Mediane. Zusätzlich werden die Effektstärken berechnet und mit vergleichbaren Studien, fachspezifischen Grenzen oder Cohen (1998/1992) eingeordnet.

Beispielformulierung:

Der Friedman-Test zeigt unterschiede des Testscores über die 3 Zeitpunkte:(Chi² (2) = 28.8, p < .001, W = 0.24.
Unterschiede waren nach Bonferroni-Korrektur beobachtbar: T1 (Mdn = 23) und T2 (Mdn = 27.5) mit p < .001, r = 0.497 sowie bei T1 und T3 (Mdn = 28) mit p < .001, r = 0.646).
Beide Effekte sind nach Cohen (1992) stark. *Zur Berechnung von r wurde für N die Anzahl der paarweisen Beobachtungen verwendet.

8 Literatur

• Cohen, J.: Statistical Power Analysis for the Behavioral Sciences (1988), S. 79-81
• Fritz, Catherine O., Peter E. Morris, and Jennifer J. Richler. “Effect size estimates: current use, calculations, and interpretation.” Journal of experimental psychology: General 141.1 (2012): 2.
• Friedman, M.: The Use of Ranks to Avoid the Assumption of Normality Implicit in the Analysis of Variance. In: Journal of the American Statistical Association. 32(200)/1937, S. 675–701
• Friedman, M.: A Correction: The Use of Ranks to Avoid the Assumption of Normality Implicit in the Analysis of Variance. 34(205)/1939, S. 109
• Schapiro Grosof, M., Sardy, H. (2014). A Research Primer for the Social and Behavioral Sciences. UK: Elsevier Science.

9 Videotutorials