Fehler 1. Art, auch Alpha-Fehler (α-Fehler), und Fehler 2. Art, auch Beta-Fehler (β-Fehler), sind statistische Konzepte zur Bezeichnung von Fehlentscheidungen bei Hypothesentests.
Das Grundproblem mit dem wir uns bei Hypothesentests in der Statistik typischerweise herumschlagen müssen ist, dass wir nur eine Stichprobe zur Verfügung haben. Wenn wir also beispielsweise einen Mittelwertvergleich wie den t-Test durchführen dann haben wir lediglich eine kleine Stichprobe und das was wir in der Stichprobe an Erkenntnissen und Ergebnissen generieren können, das müssen wir auch versuchen irgendwie auf die Grundgesamtheit übertragen zu können. Die Frage, die im Raum steht: gilt der gefundene Zusammenhang in unserer Stichprobe auch für die Grundgesamtheit? Diese Frage kann man versuchen mit Hilfe von Fehler 1. Art und Fehler 2. Art zu beantworten.
Inhaltsverzeichnis
1 Ein Einführungsbeispiel zu Fehler 1. Art und Fehler 2. Art
Ein kleines Beispiel hierzu soll das ganze etwas näher verdeutlichen. Wir haben aus welchen Gründen auch immer die Behauptung aufgestellt, dass 30 % der deutschen Bevölkerung Volksmusik mögen. Nun wollen wir dies versuchen zu verifizieren oder auch zu verwerfen und das funktioniert, indem wir eine Stichprobe erheben und jene prüfen.
Wir gehen also morgens beispielsweise in eine Apotheke und befragen die Kunden, die hereinkommen, ob sie Volksmusik mögen oder nicht. Das Ergebnis überrascht uns etwas, denn 80 % mögen Volksmusik. Uns fällt dabei aber auf, dass wir hauptsächlich Rentner befragen, weil Rentner natürlich morgens Zeit haben. Die arbeitende Bevölkerung werden wir in der Regel nicht antreffen und auch Kinder werden morgens nicht allein in die Apotheke gehen. Demzufolge ist das Ergebnis von 80% schon etwas sehr hoch. In Wahrheit, wo auch immer diese Zahl jetzt herkommt, haben wir in Erfahrung bringen können, dass nur 25% der Deutschen Volksmusik mögen.
Wir sehen also, dass die Behauptung, das Ergebnis und die tatsächliche Wahrheit, wenn man sie so nennen möchte, durchaus nicht übereinstimmen. Wie kann man das Ganze jetzt mit dem Fehler 1. Art und Fehler 2. Art in Verbindung bringen?
2 Nullhypothese und Alternativhypothese
Die Nullhypothese (H0) ist immer die Hypothese, die wir falsifizieren, also verwerfen wollen. Gelingt uns dies, können wir die Alternativhypothese (H1) annehmen. Eine typische Nullhypothese wäre, dass höchstens 25 % der Deutschen Volksmusik mögen. Die Alternativhypothese ist demnach, dass weniger als 25% der Deutschen Volksmusik mögen. Je nachdem, ob die Nullhypothese oder Alternativhypothese wahr ist und für welche der beiden wir uns entscheiden, bekommen wir eine 2×2-Tabelle, die unsere vier möglichen Entscheidungen zusammenfasst:
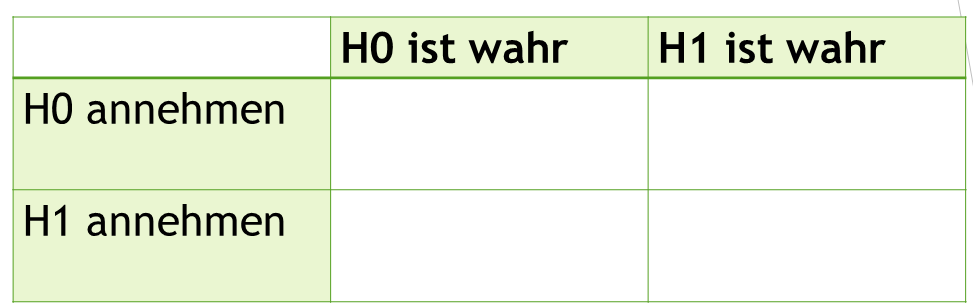
Unsere Nullhypothese (H0) kann in der Realität wahr sein, sie kann aber auch falsch sein. Wenn die Nullhypothese nicht wahr ist, gilt die Alternativhypothese (H1). Das sehen wir in dieser Tabelle in der ersten Zeile eingeblendet mit H0 ist wahr, also die Nullhypothese stimmt. Oder H1 ist wahr, also die Nullhypothese stimmt nicht:
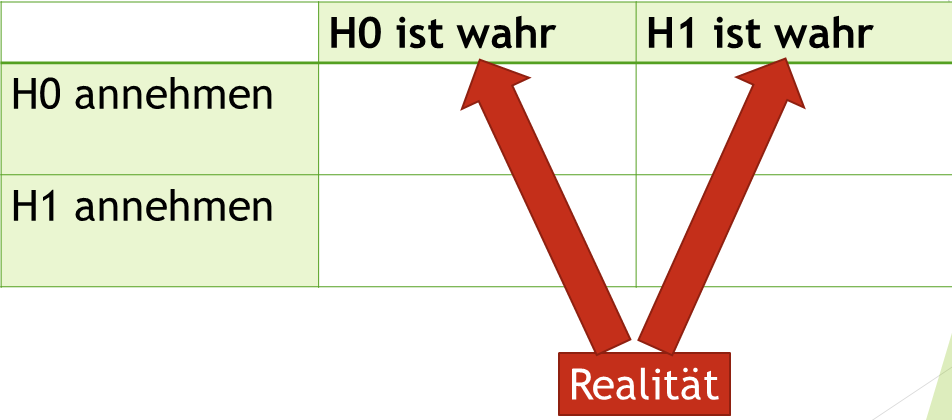
In einem Hypothesentest entscheiden wir uns nun in der ersten Spalte für Nullhypothese (H0) oder Alternativhypothese (H1). Wir haben also festgestellt das wir entweder die Nullhypothese annehmen oder verwerfen:
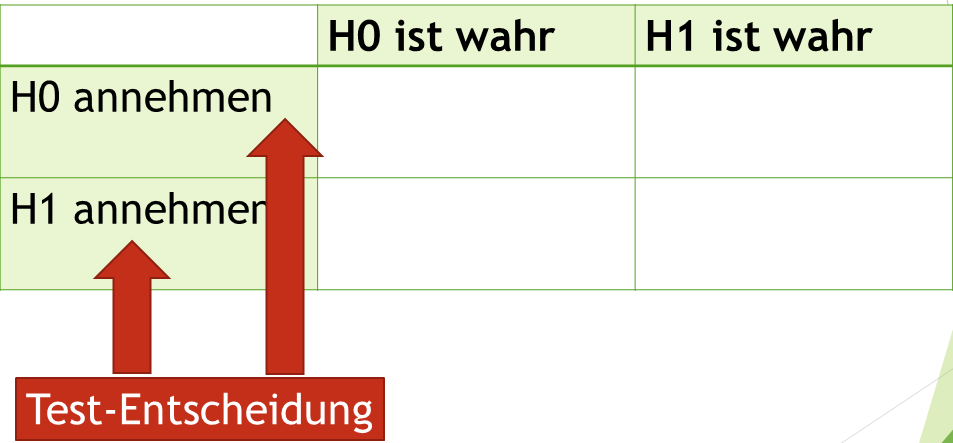
Je nachdem, was die Realität ist (Spalte) und was die Test-Entscheidung ist (Zeile), begehen wir entweder einen Fehler oder nicht.
a) H0 ist in der Realität wahr und wir nehmen sie nach einem Test an.
b) H0 ist in der Realität wahr und wir nehmen sie nach einem Test nicht an – wir verwerfen sie zugunsten von H1.
c) H1 ist in der Realität wahr und wir nehmen sie nach einem Test an.
d) H1 ist in der Realität wahr und wir nehmen sie nach einem Test nicht an – wir behalten H0 bei.
Die einzelnen vier Fälle von Hypothesenentscheidungen arbeiten wir nun durch und bringen sie Alpha-Fehler und Beta-Fehler in Verbindung.
2.1 H0 ist wahr und wird angenommen (a)
Wenn wir die Nullhypothese (H0) annehmen, sie also nicht zugunsten der Alternativhypothese (H1) verwerfen, und die Nullhypothese in der Realität wahr ist, haben wir alles richtig gemacht. Richtige Entscheidung.
Einfach gesagt: Wir nehmen H0 richtigerweise an.
2.2 H0 ist wahr und wird aber verworfen (b)
Wenn wir die Nullhypothese (H0) zugunsten der Alternativhypothese (H1) verwerfen, die Nullhypothese aber der Realität entspricht, haben wir einen Fehler gemacht. Das ist der Fehler 1. Art (Alpha-Fehler).
Einfach gesagt: Wir verwerfen H0 fälschlicherweise.
2.3 H1 ist wahr und wird angenommen (c)
Wenn wir die Nullhypothese (H0) verwerfen (und damit die Alternativhypothese (H1) annehmen) und die Alternativhypothese der Realität entspricht, haben wir alles richtig gemacht. Richtige Entscheidung.
Einfach gesagt: Wir nehmen H1 richtigerweise an.
2.4 H1 ist wahr und wird aber verworfen (d)
Wenn wir die Nullhypothese (H0) annehmen, also sie nicht zugunsten der Alternativhypothese (H1) verwerfen, und die Nullhypothese in der Realität aber falsch ist, haben wir einen Fehler gemacht. Das ist der Fehler 2. Art (Beta-Fehler)
Einfach gesagt: Wir verwerfen H1 fälschlicherweise.
3 Eine Übersicht der Entscheidungen und resultierender Fehler
Die 4 eben erläuterten Entscheidungen kann man nun einfach in die obige Tabelle einsetzen. a) und c) sind die richtigen Entscheidungen. Wir entscheiden uns im Test für die tatsächlich geltenden Hypothesen. b) und d) sind hingegen falsche Entscheidungen, wo die jeweils tatsächlich geltenden Hypothesen verworfen werden. Der Fall b) ist hierbei der Alpha-Fehler, Fall d) der Beta-Fehler.
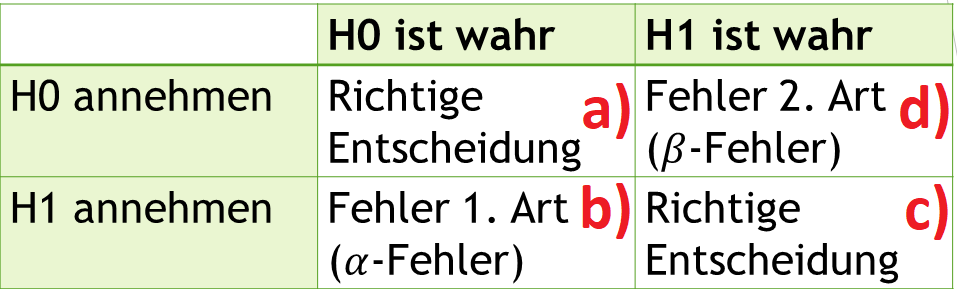
Die entscheidende Frage ist, wie hoch sind Alpha-Fehler (Fall b) und Beta-Fehler (Fall d)?
3.1 Der Fehler 1. Art (Alpha-Fehler) in Zahlen
Wenn ihr euch an eure Statistik-Vorlesung zurück erinnert, dann habt ihr häufig etwas von einem Alpha-Fehler von 0,05 gehört also 5%. Beziehungsweise schaut ihr immer, ob der p-Wert, also die statistische Signifikanz unter diesen “magischen” 5% (teilweise auch 1%) liegt. Diese Schwelle ist euer Alpha-Fehler. Das heißt das Verwerfungsniveau oder die Verwerfungswahrscheinlichkeit der Nullhypothese ist 5% (oder 1%) und damit begeht ihr also wissentlich zu 5% (oder 1%) einen Fehler 1. Art. Ihr verwerft also H0, obwohl sie gilt. Damit ist auch klar, warum man die Grenze, ab der man eine Nullhypothese verwirft, eher klein wählen sollte. Ist euer Alpha 10%, begeht ihr also zu 10% einen Fehler 1. Art. Das ist schon recht viel. Wenn ihr nun noch mehrere paarweise Vergleiche im Rahmen einer ANOVA habt und nicht für den Alphafehler mit einem Post-hoc-Test kontrolliert, kommt ihr ganz schnell sehr wahrscheinlich zu Fehlentscheidungen.
Einfach gesagt: euer Alpha, zu dem ihr Hypothesen verwerft, ist euer Alpha-Fehler. Der Alpha-Fehler ist die Wahrscheinlichkeit H0 fälschlicherweise zu verwerfen. Streng genommen ist Alpha nur eine Grenze, unter der ihr bleiben wollt. Eure Signifikanz (p-Wert) ist die tatsächliche Wahrscheinlichkeit einer Fehlentscheidung zugunsten von H1. 1-Alpha bzw. 1-p ist die Wahrscheinlichkeit richtig zu liegen. Sie wird auch Spezifität genannt. Demnach strebt man immer nach einem möglichst kleinen p-Wert, um mit möglichst hoher Wahrscheinlichkeit richtig zu liegen. Das Ziel ist hohe Spezifität.
3.2 Der Fehler 2. Art (Beta-Fehler) in Zahlen
Den Beta-Fehler zu quantifizieren ist ein viel schwierigeres Thema als ich das jetzt mit dem Alpha-Fehler kurz erklären konnte. Allein mit diesem Thema kann man bereits diverse Seiten füllen. Der Beta-Fehler beschreibt indirekt auch die sog. Power des Hypothesentests. 1-Beta ist die Power und wird auch als Teststärke bezeichnet. Die Teststärke ist die Fähigkeit eines Tests einen existierenden Effekt zu entdecken. Ein Beispiel ist der einfache t-Test und die Prüfung auf einen Unterschied zwischen zwei Gruppen. Je höher Beta, desto niedriger ist die Teststärke (1-Beta). Demzufolge sollte es das Ziel sein, einen möglichst kleinen Beta-Fahler zu haben, damit man wiederum eine möglichst hohe Teststärke hat. Dies wird auch Sensitvität genannt. Das Ziel ist stets hohe Sensitivität, also hohe Power.
Paradoxerweise steigt Beta – um beim Beispiel des Unterschieds bei zwei Gruppen zu bleiben – bei nur kleinen Unterschieden stark an. Salopp gesagt: der Test hat Probleme zu erkennen, ob der kleine Unterschied systematisch oder zufällig ist. Um sicher zu sein, braucht der Test größere Stichproben/Gruppen. Beta wird im Vorfeld eines Tests typischerweise auf 5% festgelegt und dann bei gewünschte Effektstärke (= Größe des Unterschieds der beiden Gruppen, z.B. Cohen’s d) geschätzt, wie groß die Stichprobe mindestens sein muss. Das geschieht recht einfach mit z.B. GPower.
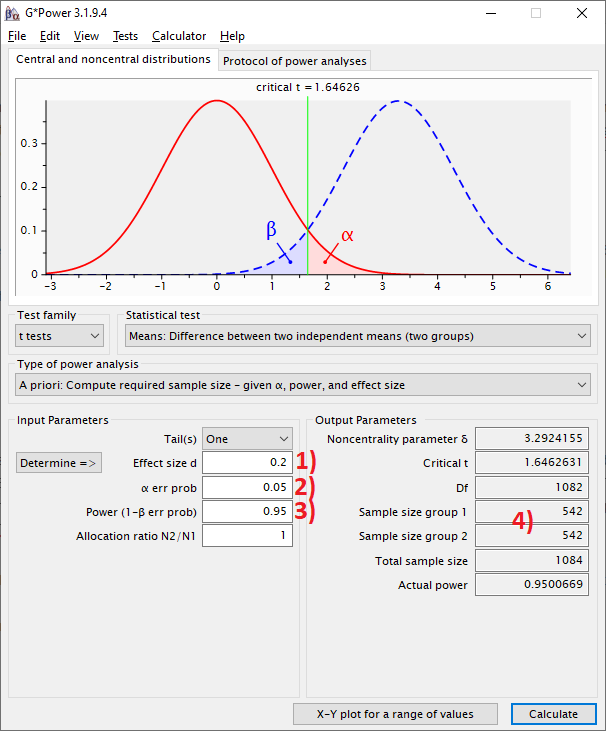
Ein Power-Beispiel – ein kleiner Unterschied
1) in Abbildung: eine geringe Effektstärke (= Unterschied zwischen den beiden Gruppen) von Cohen’s d = 0,2
2) Alphafehler 0,05, also 5% und
3) einer gewünschten Power von 95% ergeben sich
4) n=542 je Gruppe, also insgesamt n=1084.
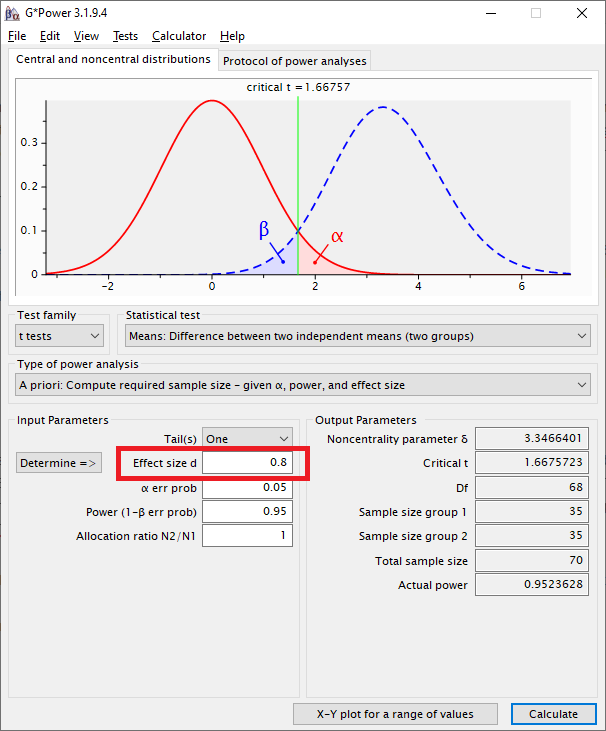
Ein Power-Beispiel – ein großer Unterschied
Verändere ich jetzt lediglich die Effektstärke, also wie stark der Unterschied ist, hin zu einem größeren Wert von Cohen’s d (von 0,2 auf 0,8), sinkt die notwendige Gruppengröße drastisch auf n=35 bzw. die Stichprobengröße auf n=70.
Wie ihr seht, ist der Beta-Fehler ein heikles Thema, das sehr mit Vorsicht zu behandeln ist. Neben der im Vorfeld notwendigen Stichprobengröße kann alternativ die Power auch im Nachgang ermittelt werden. Dieses Vorgehen ist aber nicht frei von Kritik und nur unter ganz bestimmten Umständen überhaupt sinnvoll (vgl. O’Keefe (2010)).
4 Ein Merksatz zum Schluss
Beta-Fehler: Beibehalten von H0, obwohl sie nicht gilt
5 Literatur
- Daniel J. O’Keefe (2007) Brief Report: Post Hoc Power, Observed Power, A Priori Power, Retrospective Power, Prospective Power, Achieved Power: Sorting Out Appropriate Uses of Statistical Power Analyses, Communication Methods and Measures, 1:4, 291-299
6 Videotutorial


