Inhaltsverzeichnis
1 Ziel des Einstichproben-Wilcoxon-Test in SPSS
Der Einstichproben-Wilcoxon-Test ist die nicht-parametrische Alternative zum Einstichproben t-Test. Er prüft, ob der Median der vorliegenden Variable bzw. Verteilung verschieden von einem bestimmten Wert ist.
2 Voraussetzungen des Einstichproben-Wilcoxon-Test in SPSS
- Eine ordinal oder metrisch skalierte Variable – Normalverteilung ist keine Voraussetzung.
- Die Fälle sollten unabhängig voneinander sein.
- Ein vermuteter Median, gegen den getestet wird. Dieser ergibt sich aus der Grundgesamtheit, bisherigen Erfahrungen oder schlicht (theoretisch hergeleiteten) Vermutungen.
3 Durchführung des Einstichproben-Wilcoxon-Test in SPSS – ein Beispiel
Die Nullhypothese beim Einstichproben Wilcoxon-Test geht stets von Gleichheit der Mediane von Stichprobe und Grundgesamtheit aus.
Ihr könnt bei diesem Test einseitig und zweiseitig testen. Einseitig heißt lediglich, dass eine konkrete Vermutung im Vorfeld existiert. Also zum Beispiel vermutet man, dass der Stichprobenmedian kleiner oder größer ist als der Median der Grundgesamtheit. Standardmäßig wird immer zweiseitig getestet, das heißt ihr vermutet einen Unterschied. Ob der Median der Stichprobe größer oder kleiner als der Median der Grundgesamtheit ist, wisst ihr allerdings nicht.
Der Wilcoxon-Test für eine Stichprobe ist zu finden unter Analysieren -> Nicht parametrische Tests -> Eine Stichprobe.
Im Anschluss erhält man ein schlichtes Dialogfeld. Hier ist der Reiter Felder auszuwählen. Das Feld Testvariable ist standardmäßig mit allen Variablen gefüllt. Demzufolge sind alle Variablen zu löschen, die ihr NICHT testen wollt. Ich möchte hier die Motivation testen und belasse sie im Feld Testvariable. Sie ist in meinem Fall zwischen 1 und 10 skaliert.
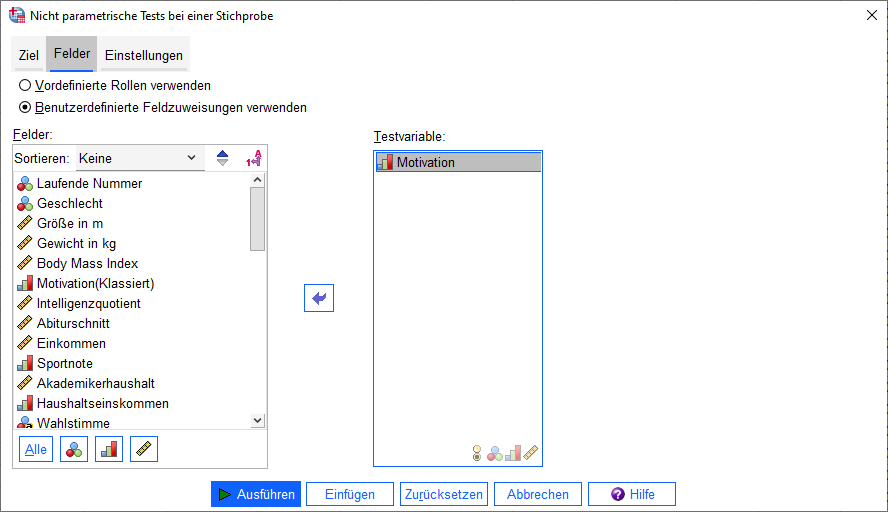
Als Nächstes wird der Reiter Einstellungen ausgewählt. Dann wird Tests anpassen selektiert und der Haken bei (Median- und hypothetische Werte vergleichen (Wilcoxon-Test)) gesetzt. Nun ist noch ein Hypothetischer Median einzutragen. Da ich im Vorfeld keine Daten habe und einfach von einer Gleichverteilung der 10 Ausprägungen ausgehe, ist der Median 5,5. Auf diesen Median hin teste ich nun.
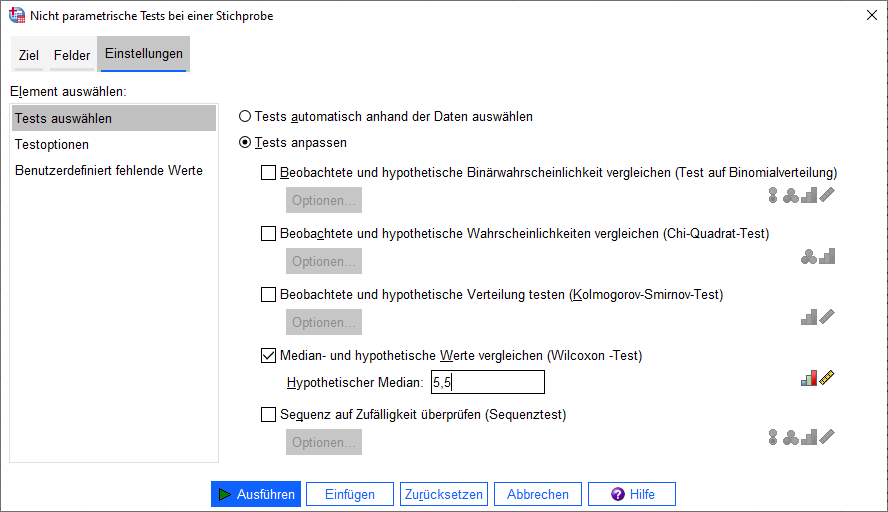
4 Interpretation der Ergebnisse des Einstichproben Wilcoxon-Tests
Nach Klick auf Ausführen erhält man eine kleine Übersicht an Ergebnistabellen. Die erste und wichtigste ist die Tabelle Hypothesenübersicht. Hier steht noch mal die Nullhypothese. Hier ist allerdings zu beachten, dass die Zahl gerundet dargestellt wird – es wird allerdings exakte, also mit Komma gerechnet. Das Ergebnis der Prüfung erhält man auf Basis der Signifikanz (Sig). Diese liegt mit p = 0,192 über der typischen Verwerfungsgrenze von Alpha = 0,05. Somit ist die Nullhypothese beizubehalten. Es muss von einer ungefähren Gleichheit der Stichprobe mit dem hypothetischen Median ausgegangen werden.

Das wird in der nachfolgenden Tabelle auch noch mal deutlich, wo die standardisierte Teststatistik (1,303), welche als Basis zur Berechnung der Asymptotischen Signifikanz dient, angezeigt wird.

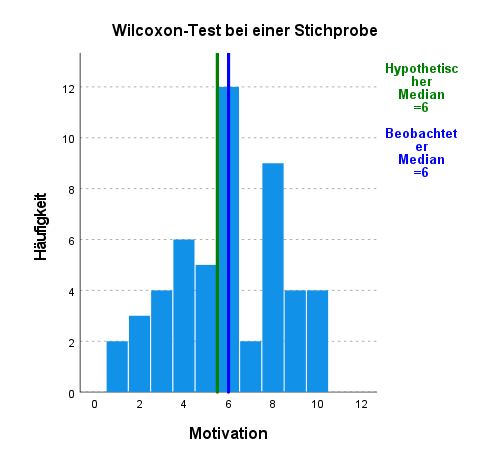
Schließlich wird noch ein Histogramm erstellt. Hier sind die Häufigkeiten der jeweiligen Merkmalsausprägungen als Säulen abgetragen, was auch einen ganz guten Überblick liefert. Der beobachtete Median (blau) liegt bei glatt 6. Der hypothetische Median (grün) liegt bei 5,5. Erneut hier der Hinweis, dass die 6 beim hypothetischen Median nur gerundet dargestellt ist. Es ist auch im Histogramm ersichtlich, dass sich die beiden Median nur bedingt unterscheiden – zu wenig für den Test – salopp gesagt.
5 Effektstärke ermitteln
Die Effektstärke r wird mit folgender Formel berechnet. Der z-Wert wird durch die Wurzel der Stichprobengröße geteilt. Aufgrund der Betragsstriche wird dieser Quotient immer positiv sein.
![]()
Wo bekommt man nun aber den z-Wert her? Der z-Wert ist die standardisierte Teststatistik aus der zweiten Tabelle (im Beispiel 1,303), die Stichprobengröße kann ebenfalls bei Gesamtzahl (hier: 51) abgelesen werden.
Da ich im Beispiel die Nullhypothese nicht verwerfen kann, darf keine Effektstärke berechnet werden. Wo kein Unterschied (=Effekt), da ist auch keine Stärke des Unterschiedes (Effektstärke) zu berechnen.
Habt ihr die Nullhypothese verwerfen können, verwendet ihr Cohen: Statistical Power Analysis for the Behavioral Sciences (1988), S. 79-81 für die Einordnung. Die Effektgrenzen sind:
- ab 0,1: schwacher Effekt
- ab 0,3: mittlerer Effekt
- ab 0,5: starker Effekt
6 Tipp zum Schluss
Findest du die Tabellen von SPSS hässlich? Dann schau dir mal an, wie man mit wenigen Klicks die Tabellen in SPSS im APA-Standard ausgeben lassen kann.
7 Videotutorial


