Inhaltsverzeichnis
1 Ziel des Einstichproben t-Test in SPSS
Der Einstichproben t-Test prüft, ob der Mittelwert eines Merkmals einer Stichprobe dem Mittelwert einer Grundgesamtheit oder einem vermuteten Mittelwert gleich bzw. in etwa ähnlich ist. Hiermit kann man prüfen, ob eine Schulklasse in etwa so intelligent wie die Grundgesamtheit ist. In diesem Artikel zeige ich, wie man den Einstichproben t-Test in SPSS rechnet und die Ergebnisse interpretiert. Kein SPSS? Kein Problem! Hier geht es zum Artikel in Excel oder R – jeweils mit Beispielberechnung.
2 Voraussetzungen des Einstichproben t-Test in SPSS
- Man braucht lediglich eine metrisch, also intervall- oder verhältnisskalierte Variable.
- Diese Variable sollte in etwa normalverteilt sein. Wie man eine Variable auf Normalverteilung prüft, zeigt dieser Artikel. Aus Vereinfachungsgründen zeige ich dies in diesem Artikel nicht und gehe schlicht von Normalverteilung aus.
- Die Fälle sollten voneinander unabhängig sein.
- Es braucht zudem einen vermuteten Mittelwert. Dieser ergibt sich aus der Grundgesamtheit, bisherigen Erfahrungen oder schlicht (theoretisch hergeleiteten) Vermutungen.
3 Durchführung des Einstichproben t-Test in SPSS – ein Beispiel
3.1 Nullhypothese
Die Nullhypothese beim Einstichproben t-Test geht stets von Gleichheit der Mittelwerte von Stichprobe und Grundgesamtheit aus.
Ihr könnt bei diesem Test einseitig und zweiseitig testen. Einseitig heißt lediglich, dass eine konkrete Vermutung im Vorfeld existiert. Also zum Beispiel vermutet man, dass der Stichprobenmittelwert kleiner oder größer ist als der Mittelwert der Grundgesamtheit. Standardmäßig wird immer zweiseitig getestet, das heißt ihr vermutet einen Unterschied. Ob der Mittelwert der Stichprobe größer oder kleiner als der Mittelwert der Grundgesamtheit ist, wisst ihr allerdings nicht.
3.2 t-Statistik
Die Berechnung der T-Statistik ist die Basis, die folgende Formel hat:
![]()
Zum Glück muss man das in SPSS nicht alles nachbauen. Der Test ist zu finden unter Analysieren -> Mittelwerte vergleichen -> t-Test bei einer Stichprobe.
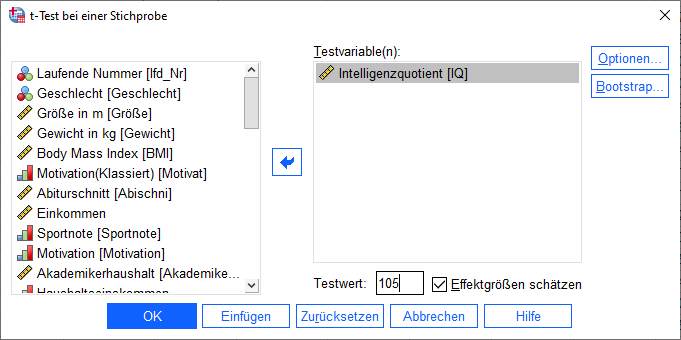
Danach erhält man ein schlichtes Dialogfeld, wo man die Testvariable eingeben kann. Ich möchte den Intelligenzquotient (IQ) testen und füge ihn daher hinzu.
Als nächstes brauche ich einen Testwert, den ich unten eintrage. Wie bereits erwähnt, ist es hierfür notwendig im Vorfeld eine Vermutung oder Erfahrungswerte zu haben. In meinem Fall habe ich in einer größeren Stichprobe einer Vergleichsstudie einen mittleren IQ von 105 beobachtet und wähle diesen als Vergleichs- bzw. Testwert.
4 Interpretation der Ergebnisse des Einstichproben t-Test in SPSS
Zunächst erhält man eine kleine Tabelle mit deskriptiven Statistiken, also Anzahl an Beobachtungen (N) Mittelwert, Standardabweichung sowie Standardfehler des Mittelwertes. Hier ist eigentlich nur der Mittelwert interessant. Der beträgt hier 109,82 und ist an sich größer als die vermuteten 105. Die Frage ist, ob es sich um einen signifikanten Effekt handelt bzw. ob wir einen “zufälligen Unterschied” ausschließen oder mit zumindest recht kleiner Irrtumswahrscheinlichkeit beobachten.

4.1 Interpretation des zweiseitigen t-Tests
Die nächste Tabelle ist die Ergebnistabelle des Einstichproben t-Tests. Hier wird der T-Wert mit 2,582 bei 50 Freiheitsgraden bei einer zweiseitigen Signifikanz von p = 0,013 angegeben. Typische Schreibweise: T(50) = 2,582; p = 0,013. Der Unterschied zwischen dem beobachteten Mittelwert und dem Testwert von 105 ist somit mit sehr hoher Wahrscheinlichkeit nicht zufällig, da die typische Verwerfungsgrenze von Alpha = 0,05 vom p-Wert mit p = 0,013 deutlich unterschritten wird. Die Nullhypothese wird somit verworfen und die Alternativhypothese eines Unterschiedes angenommen.

4.2 Interpretation des einseitigen t-Tests
Hat man im Vorfeld die wohlbegründete Vermutung, dass der Stichprobenmittelwert über dem vermuteten Testwert liegt, testet man einseitig. Dies bedeutet in Kurzform, dass man die Signifikanz halbieren darf. Der p-Wert ist demnach nun p = 0,0065 und noch deutlicher unter 0,05. Die Verwerfung der Nullhypothese zugunsten der Alternativhypothese wäre auch hier das Ergebnis.
ACHTUNG: Ist die Vermutung im Vorfeld ein kleinerer beobachteter Mittelwert als 105, würde man bei diesem Ergebnis von 109,82 diese Alternativhypothese nicht annehmen dürfen, weil das Ergebnis konträr zur Vermutung ist. Die Signifikanz ist hierbei kein Grund für die Annahme der Alternativhypothese!
4.3 Interpretation der Effektstärke (SPSS 27+)
Sollte man die Nullhypothese keines Unterschiedes zugunsten der Alternativhypothese eines Unterschiedes verwerfen, ist die Größe dieses Unterschiedes zu quantifizieren bzw. einzuordnen. Seit SPSS 27 wird (sofern oben der Haken gesetzt wurde) direkt die Effektstärke Cohen’s d ausgegeben. Hierbei ist der Wert der Punktschätzung maßgeblich. Im Beispiel ist es 0,362. Dieser Wert ist nun einzuordnen. Cohen: Statistical Power Analysis for the Behavioral Sciences (1988), S. 25-27 gibt die folgenden Grenzen vor:
- ab 0,2 ist es ein schwacher Effekt
- ab 0,5 ist es ein mittlerer Effekt
- ab 0,8 ist es ein starker Effekt

Somit ist die Effektstärke, also die Größe des Unterschiedes mit 0,362 unter der Grenze zum mittleren Effekt. Demzufolge ist der Unterschied klein.
Berechnung und Interpretation der Effektstärke (SPSS 26 und früher)
Die Effektstärke wird von früheren Versionen von SPSS nicht ausgegeben und muss händisch berechnet werden. Die Berechnung erfolgt über die Formel mit dem T-Wert geteilt durch die Wurzel aus der Anzahl der Beobachtungen (N).
![]()
Im Beispiel ist der t-Wert 2,582 und die Freiheitsgrade (df) 50. Eingesetzt in die Formel:
![]()
Das Ergebnis gleicht natürlich der obigen Berechnung. Der Unterschied ist damit auch hier mittel.
5 Reporting des Einstichproben t-Tests
Probanden der Stichprobe (M = 109,82; SD = 13,34) haben einen vom Vergleichswert 105 verschiedenen IQ, t(50) = 2,58; p = 0,013; d = 0,36.
Nach Cohen (1992) ist dieser Unterschied klein.
6 Videotutorials
Literatur
- Effektstärkengrenzen: Cohen, J. (1988): Statistical Power Analysis for the Behavioral Sciences. bzw.
- Cohen, J. (1992). A power primer. Psychological bulletin, 112(1), 155-159.


