Statistische Tests haben zwei grundlegende Hypothesen. Zum einen die Nullhypothese, die verworfen werden kann. Zum anderen die Alternativhypothese, die bei Verwerfung der Nullhypothese angenommen wird. Gelingt es nicht, die Nullhypothese zu verwerfen, wird jene beibehalten.
Inhaltsverzeichnis
1 Das Grundprinzip einseitiger Tests und zweiseitiger Tests
Grundlegend ist die im Vorfeld aufgestellte Hypothese dafür verantwortlich, ob man einen einseitigen oder zweiseitigen Test durchführt. Die Nullhypothese geht bei Mittelwertvergleichen und Regressionsmodellen von keinen Unterschieden bzw. Einflüssen aus. Die Alternativhypothese geht demzufolge von einem Unterschied bzw. Einfluss aus. Allerdings ist nicht klar, ob der Mittelwert steigt oder fällt oder im Falle der Regression die Variable einen positiven oder negativen Einfluss ausübt. Ist dies jedoch im Vorfeld bekannt, kann eine explizitere Alternativhypothese formuliert werden.
Ein Beispiel für einen Mittelwertvergleich: Aus bisherigen Erfahrungen ist bekannt, dass ein gewisses Training die Leistungsfähigkeit erhöht. Man hat also eine Wirkungsvermutung. Diese Wirkungsvermutung formuliert man explizit in der zu prüfenden Hypothese: “Ein Training führt zu einer erhöhten Leistungsfähigkeit”. Solch eine Hypothese nennt man auch gerichtet – sie drückt eine Wirkungsvermutung aus. Der Mittelwert des Wiederholungen einer Übung der Probanden wird nach dem Training größer sein als vor dem Training:
Im Gegensatz dazu wäre eine ungerichtete Hypothese: “Ein Training führt zu einer Änderung der Leistungsfähigkeit”. Ich kann anhand der Ungerichtetheit der Hypothese nicht erkennen, ob die Leistungsfähigkeit sinkt oder steigt:
Die Wirkungsvermutung bzw. -richtung ist demnach der ausschlaggebende Grund dafür, dass man einseitig testen kann. Hat man keine Wirkungsvermutung, verbleibt nur die zweiseitige Testung.
2 Was nützen mir einseitige Tests und zweiseitige Tests?
Die Grundidee des einseitigen Tests ist, dass man nicht prüfen muss, ob, wie im Falle des Mittelwertbeispiels von eben, der Wert gestiegen oder gefallen ist. Man muss dank der Alternativhypothese sozusagen nur “auf einer Seite schauen”. Das hat die Konsequenz, dass die Signifikanz (die SPSS zum Beispiel standardmäßig 2-seitig ausgibt) halbiert werden darf. Jene gibt die Wahrscheinlichkeit für den Fehler 1. Art (Alpha-Fehler) an. Vermutet man also, dass der Ruhepuls sinkt und er ist im Mittel tatsächlich geringer, darf man die Signifikanz bei SPSS halbieren. Alternativ könnte man auch die Alpha-Grenze (typisch 0,05 also 5%) verdoppeln – sofern man vom jeweiligen Test eine zweiseitige Signifikanz erhält.
Zusammengefasst: hat man eine Wirkungsvermutung, sollte man diese auch so explizit formulieren. Ist, in Anlehnung an das obige Beispiel, ersichtlich, dass die mittlere Anzahl Wiederholungen nach dem Training größer ist als davor und wird in SPSS der t-Test gerechnet, darf die standardmäßig ausgegebene zweiseitige Signifikanz halbiert werden. Wäre die zweiseitige Signifikanz also 0,087 und damit über dem Alphaniveau von 0,05, hätte eine Halbierung eine Signifikanz von 0,0435 zur Folge und damit einen statistisch signifikanten Unterschied.
3 Ein Zahlenbeispiel
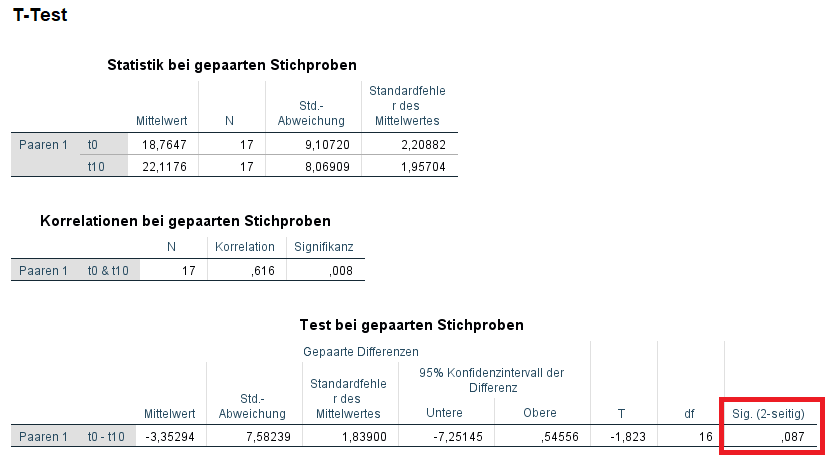
Probanden durchlaufen ein Training und müssen vor (t0) und nach dem Training (t10) Liegestütze machen. Die mittlere Anzahl der Wiederholungen der 17 Probanden liegt vor dem Training (t0) bei 18,7647. Nach dem Training (t10) liegt die mittlere Anzahl der Wiederholungen bei 22,1176. Mir war bereits im Vorfeld klar, dass sich die Probanden verbessern, weshalb ich folgende gerichtete Hypothese formuliert habe:
Der t-Test bei gepaarten/verbundenen/abhängigen Stichproben weist eine Signifikanz von 0,087 aus. Da ich aber im Vorfeld eine gerichtete Hypothese aufgestellt habe, darf ich jetzt einseitig testen. Ich muss nicht mehr schauen, ob es eine größere oder geringere Anzahl an mittleren Wiederholungen gibt – was der t-Test in SPSS standardmäßig macht. Stattdessen muss ich lediglich schauen, ob es eine höhere Anzahl ist. Aufgrund dessen darf ich die Signifikanz (2-seitig), die unten rot markiert ist, halbiert. Statt 0,087 und damit nicht statistisch signifikanter Unterschied, habe ich nun 0,0435 und damit statistisch signifikant Unterschied.