G*Power ist ein kostenloses Tool der Uni Düsseldorf. Es dient primär zur Ermittlung der Mindeststichprobengröße für ein bestimmtes statistisches Analyseverfahren.
Inhaltsverzeichnis
1 Vorbemerkungen zu Inputparametern von G*Power
G*Power dient mir vor der Datenerhebung festzustellen, wie große meine Stichprobe mindestens sein muss.
Dazu muss ich im Vorfeld bereits folgendes wissen:
- Hypothese
- Untersuchungsmethode (abgeleitet aus der Hypothese)
- Effektstärke (später mehr)
- Alpha-Fehler-Niveau
- Angestrebte statistische Power (= Teststärke)
1.1 Hypothese
Eigentlich ziemlich trivial, aber ohne Hypothese, weiß man ja gar nicht, was man untersucht. Deswegen bedarf es im Vorfeld einer (konzeptionellen) Herleitung der Hypothese(n). Hier unterscheidet man Zusammenhangshypothesen, Unterschiedshypothesen und Veränderungshypothesen. Die Art der Hypothese bestimmt die Untersuchungsmethode.
1.2 Untersuchungsmethode
- Zusammenhangshypothesen untersucht man im ungerichteten Fall mit Korrelationsanalysen. Sind Zusammenhangshypothesen gerichtet, werden typischerweise Regressionsanalysen gerechnet.
- Bei Unterschiedshypothesen werden Mittelwertvergleiche zwischen zwei (z.B. t-Test, U-Test) oder mehr (z.B. ANOVA, Kruskal-Wallis-Test) unabhängigen Gruppen gerechnet. Hat man nur zwei Gruppen, kann die Hypothese ebenfalls gerichtet sein.
- Veränderungshypothesen haben eine größere Zahl an Analysemethoden, im einfachsten Fall sind es Mittelwertvergleiche mit einer (z.B. t-Test bei verbundenen Stichproben, Wilcoxon-Test) oder mehr als einer Messwiederholungen (z.B. ANOVA mit Messwiederholung, Friedman-Test)
1.3 Effektstärke
Im Vorfeld benötigt man die Effektstärke, also wie stark der beobachtete Effekt wohl sein wird bzw. vermutet wird. Hier orientiert man sich an den Größen nach Cohen (1988). Es gibt hierzu verschiedene Herangehensweisen zur Festlegung:
- Der einfachste Weg ist eine Orientierung an Vergleichsstudien und Verwendung der dort angegebenen Effektstärke. Sollte keine angegeben sein, kann man die mitunter nachträglich mit den angegebenen Populationsparametern ermitteln.
- Der praktische Weg ist das Festlegen auf Basis der Erfahrung des Forschers. Dies ist aber subjektiv und eine Begründung mit persönlicher Erfahrung kann bei Gutachtern schnell zu einer ablehnenden Haltung führen.
- Der pragmatische Weg ist die Annahme eines mittleren Effektes. Auch hier ist eine Begründung notwendig und kann nicht einfach so getroffen werden – nicht selten findet man aber keine.
1.4 Alpha-Fehler
Der Alpha-Fehler (auch Fehler 1. Art) ist das fälschliche Ablehnen der Nullhypothese. Typisch ist als Grenze für Alpha 5% (0,05). Man akzeptiert also eine maximale Alpha-Fehlerwahrscheinlichkeit von 5%. Weitere typische Grenzen sind 1%, 0,1% oder sogar 10%. Achtung, es kommt hier häufig auf den Kontext an. Niedriger kann pauschal als besser erachtet werden – es geht ja um die Fehlervermeidung.
1.5 Statistische Power (Teststärke)
Teststärke (sog. statistische Power) beschreibt die Fähigkeit eines Tests, einen in der Stichprobe tatsächlich vorhandenen Effekt auch erkennen zu können und ist essenziell – nur leider ist das zu wenig bekannt. Die Power berechnet sich aus 1 abzüglich des Beta-Fehlers.
Der Beta-Fehler beschreibt das fälschliche Beibehalten der Nullhypothese. Hier kann man gut erkennen, dass Power und Beta-Fehler (auch Fehler 2. Art) direkt zusammenhängen. Ich erhöhe die Power, wenn ich den Beta-Fehler minimiere. Auch hier sind 5% Fehlerwahrscheinlichkeit erstrebenswert, somit ist die Power 1 – 0,05 = 0,95 (95%). Mehr ist kaum praktikabel. Als Kompromiss findet man als Untergrenze 0,8, also 80%. Eine geringere Power im Vorfeld anzunehmen, ist kaum rechtfertigbar.
2 Eingabe in G*Power

Das Fenster sieht recht nüchtern aus. Wichtig sind 3 Dinge:
2.1 Testfamilie und statistischer Test
Testfamilie ist die einem Test zugrunde liegende Verteilung. Wenn man dies nicht weiß, ist das kein Problem und man kann im oberen Reiter “Tests” das Verfahren direkt auswählen. Testfamilie und statistischer Test werden dann ausgefüllt.
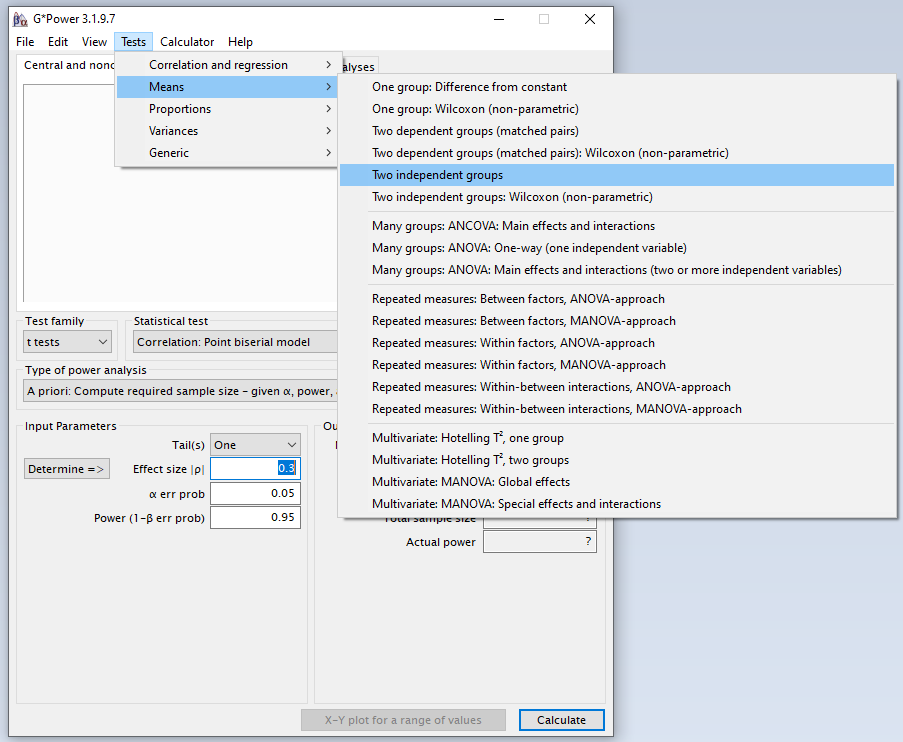
2.2 Art der Poweranalyse
Hier gibt es verschiedene Möglichkeiten. Allen voran A priori sowie Compromise , Criterion, Post hoc und Sensitivity.
An dieser Stelle ist für die Planung der Mindeststichprobengröße A priori auszuwählen. Andere Verfahren sind eher unüblich. Besonders post hoc sollte nicht gerechnet werden, weil man sehr schnell in Versuchung gerät, falsche Schlüsse zu ziehen. Besonders beliebt ist eine niedrige Power für Nichtsignifikanz verantwortlich zu machen. Ein Fehlschluss, denn Power steigt mit sinkender Signifikanz des Tests bei konstanter Effektgröße. Aberson (2019): “[…] if we find that post hoc power is low, all we know is that the observed effect size was too small to be detected with the design we used.” Zhang et al. (2019) sowie viele weitere Autoren diskutieren post hoc Poweranalysen und warum man sie nicht rechnen sollte.
2.3 Inputparameter
Ich hatte bereits oben ein-/zweiseitige Tests, Effektstärke, Alpha-Fehler und Power erörtert. Entsprechend sind diese hier einzutragen. Unter Tails(s) steht “one” für einseitig, “two” entsprechend für zweiseitig.
Effect size ist je nach Verfahren eine andere. Im Beispiel ist es für den t-Test bei unabhängigen Gruppen Cohens d. Hält man die Maus auf dem Eingabefeld, werden via Tooltip die Grenzen noch mal eingeblendet.
Alpha-Fehler-Wahrscheinlichkeit ist die Wahrscheinlichkeit, die Nullhypothese fälschlicherweise abzulehnen und sollte aus Erfahrung nicht größer als 0,05 (5%) sein.
Power sollte möglichst groß sein, evtl. ist auch eine Power von 0,8 rechtfertigbar. Die Limitierung des Beta-Fehlers sollte aber im Vordergrund stehen, damit die Nullhypothese nicht fälschlicherweise beibehalten wird und ein vorhandener Effekt nicht erkannt wird. Findet man auch bei vergleichsweise niedriger Power eine Signifikanz, liegt das meist an einem hinreichend großen Effekt, also großer Effektstärke.
Bei manchen Tests sind zusätzlich noch andere Variablen wie Allocation ratio (Gruppenverhältnisse), df (degrees of freedom – Freiheitsgrade), Number of groups (Anzahl Gruppen), Number of covariates (Anzahl Kontrollvariablen), Number of predictors (Anzahl unabhängige Variablen) usw. anzugeben.
3 Outputparameter von G*Power
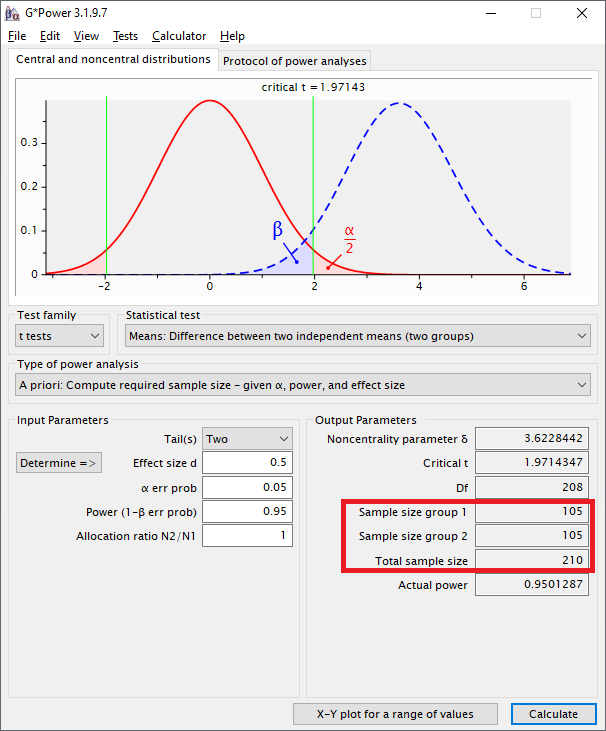
Je nach Testverfahren, wofür die Mindeststichprobengröße ermittelt wird, sieht der Output etwas anders aus. Für das Beispiel des t-Tests wird die Gesamtstichprobengröße noch mals für die jeweiligen Gruppen unterteilt angegeben. Wenn unter allocation ratio ein Wert verschieden von 1 angegeben wird, sind die Gruppengrößen entsprechend auch unterschiedlich.
4 Videotutorial
5 Literatur
- Cohen, J. (1988). Statistical power analysis for the behavioral sciences. New York, NY: Psychology Press, Taylor & Francis Group
- Zhang, Y., Hedo, R., Rivera, A., Rull, R., Richardson, S., & Tu, X. M. (2019). Post hoc power analysis: is it an informative and meaningful analysis?. General psychiatry, 32(4), e100069. https://doi.org/10.1136/gpsych-2019-100069
- Aberson, C. L. (2019). Applied power analysis for the behavioral sciences. Speziell: https://books.google.de/books?id=qSiFDwAAQBAJ&lpg=PT14&pg=PT35#v=onepage&q&f=false


