Inhaltsverzeichnis
1 Ziel des Chi-Quadrat-Test in SPSS
Der Chi-Quadrat-Test prüft, ob zwischen erwarteten und beobachteten Häufigkeiten statistisch signifikante Unterschiede bestehen. Hierzu werden die quadrierten Abweichungen der tatsächlichen von den erwarteten Häufigkeiten berechnet und durch die erwarteten Häufigkeiten geteilt. In SPSS wird einem dies abgenommen und direkt berechnet. Den Chi-Quadrat-Test kann man auch in Excel oder in R rechnen.
2 Voraussetzungen des Chi-Quadrat-Test in SPSS
- Zwei nominal skalierte Variablen
- 2 oder mehr Ausprägungen dieser Variablen
Fragen können unter dem verlinkten Video gerne auf YouTube gestellt werden.
3 Durchführung des Chi-Quadrat-Tests in SPSS
Über das Menü in SPSS: Analysieren -> Deskriptive Statistiken -> Kreuztabellen
In diesem Beispiel soll untersucht werden, ob sich das Abstimmverhalten von Männern und Frauen unterscheidet. Die Nullhypothese Chi-Quadrat-Tests lautet, dass sie sich nicht unterscheiden. Für einen Unterschied ist die Nullhypothese also zu verwerfen.
Welche Variable bei Zeilen(n) und Spalten aufgenommen wird, ist prinzipiell euch überlassen. In diesem Beispiel ist das Geschlecht (mit 0 und 1 codiert) in die Zeile und die Stimme (ebenfalls mit 0 und 1 codiert) in die Spalte verschoben.
Bei der Schaltfläche Statistiken wird ganz oben Chi-Quadrat ausgewählt
und mit weiter zum Dialogfeld Kreuztabellen zurückgekehrt.
Bei der Schaltfläche Zellen empfiehlt sich neben “Beobachtet” auch “Erwartet” anzuhaken und mit weiter zum Dialogfeld Kreuztabellen zurückzukehren.
Abschließend kann im Dialogfeld Kreuztabellen OK geklickt werden, um die Berechnung auszuführen.
4 Interpretation der Ergebnisse des Chi-Quadrat-Test in SPSS
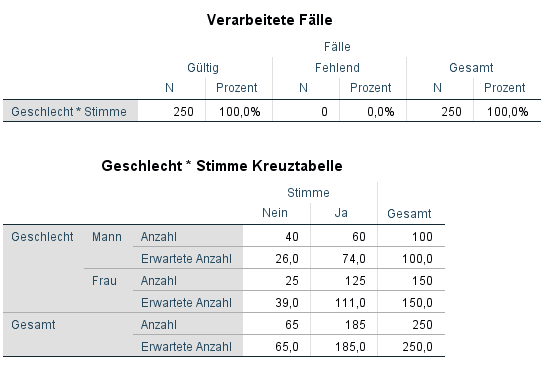
Die obere Tabelle “Verarbeitete Fälle” gibt einen Überblick über die Anzahl an Fällen, die im Test analysiert werden. Im Beispiel 250.
Darunter findet sich die Kreuztabelle mit euren Variablen, im Falle des Beispiels Geschlecht*Stimme. Hier erlangt man bereits die ersten interessanten Erkenntnisse.
Die Tabelle zeigt, dass es insgesamt 100 Männer sind, 40 haben mit Nein, 60 mit Ja gestimmt (Zeile “Anzahl”). Bei den Frauen sind es insgesamt 150, dabei 25 mit Nein und 125 mit Ja (Zeile “Anzahl”). Die erwarteten Anzahlen stehen direkt unter der jeweiligen tatsächlich beobachteten Anzahl. Es wurde erwartet, dass 26 Männer mit Nein und 74 mit Ja stimmten (Frauen: 39 mit Nein und 111 mit Ja). Die erwarteten Häufigkeiten ergeben sich auf Basis der Randhäufigkeiten und müssen nun auf statistisch signifikanten Unterschied zu den beobachteten Häufigkeiten geprüft werden.
Hierzu ist die folgende Tabelle “Chi-Quadrat-Tests” zu interpretieren.
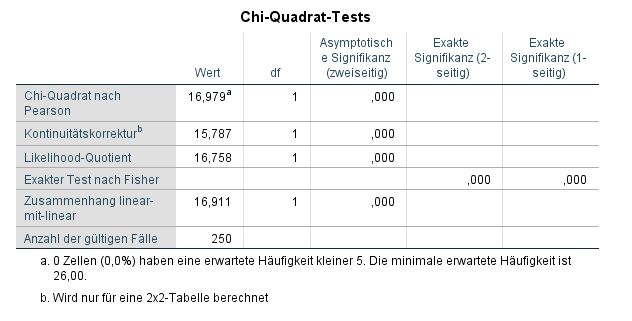
Interessant ist die erste Zeile “Chi-Quadrat nach Pearson”. Der Chi-Quadrat-Wert muss nicht interpretiert werden. In der Spalte “Asymptotische Signifikanz (zweiseitig)” ist die relevante Information, die den Chi-Quadrat-Wert entsprechend schon verarbeitet hat. Die Nullhypothese des Chi-Quadrat-Tests lautet, dass es keine statistisch signifikanten Unterschieden zwischen erwarteter und beobachteter Häufigkeit gibt. Da die Signifikanz unter 0,05 liegt (hier abgerundet: 0,000), ist diese Nullhypothese zu verwerfen. Entsprechend ist die Alternativhypothese anzunehmen, dass es statistisch signifikante Unterschiede zwischen erwarteter und beobachteter Häufigkeit gibt. Demzufolge unterscheiden sich Männer und Frauen in ihrem Abstimmverhalten.
Hinweis: Ist die erwartete Häufigkeit in einer Zelle der oberen Kreuztabelle 5 oder kleiner, ist der exakte Test nach Fisher zu interpretieren. Dieser wird in einem solchen Falle errechnet und ist aufgrund von Zellhäufigkeiten größer 5 im Beispiel von SPSS nicht errechnet worden.
5 Ermittlung der Effektstärke des Chi-Quadrat-Tests für eine 2×2-Kreuztabelle
Die Effektstärke Phi bzw. w wird bei einer 2×2-Kreuztabelle mit folgender Formel berechnet. Der Chi-Quadrat-Wert (Standardteststatistik) wird durch die Stichprobengröße geteilt und hieraus anschließend die Wurzel gezogen. Eine Effektstärke kann man sinnvollerweise allerdings nur für statistisch signifikante Unterschiede berechnen.
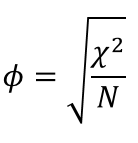
Im Beispiel ist der Chi-Quadrat-Wert 16,978517 und N 250. Das Ergebnis ist
w=0,2606 und ist ein schwacher Effekt.
Zwischen 0,1 und 0,3 ist es ein schwacher Effekt, zwischen 0,3 und 0,5 ein mittlerer Effekt und ab 0,5 ist es ein starker Effekt. Quelle: Cohen, Jacob (1988): Statistical Power Analysis for the Behavioral Sciences.
6 Ermittlung der Effektstärke des Chi-Quadrat-Tests für eine beliebige Kreuztabelle
Solltet ihr eine Kreuztabelle haben, die mehr als 2 Spalten und Zeilen hat, empfehle ich euch das Video auf meinem YouTube-Kanal, da die Menge an Formeln zu einem zu langen Artikel führen würde.
7 Videotutorials
Weitere nützliche Tutorials findest du auf meinem YouTube-Kanal.
8 Tipp zum Schluss
Findest du die Tabellen von SPSS hässlich? Dann schau dir mal an, wie man mit wenigen Klicks die Tabellen in SPSS im APA-Standard ausgeben lassen kann.


