Inhaltsverzeichnis
1 Boxplot interpretieren – was ist überhaupt ein Boxplot?
Einen Boxplot (auch Box plot, Box-Whisker-Plot oder Kastendiagramm) interpretieren – das kann man anhand der verschiedenen Streumaße und insbesondere Lagemaße einer Verteilung. Sie werden im Boxplot in einer einzigen Grafik dargestellt. Speziell für den Vergleich verschiedener Verteilungen eignet er sich recht gut, also im Vorfeld von z.B. Gruppenvergleichen.
Hinweis: Wie man einen Boxplot erstellt, zeige ich für SPSS und R separat.
Der einfachste Boxplot besteht lediglich aus 3 Dingen:
- der Box,
- den Antennen und
- dem Median.
Hinzu kommen oft noch Ausreißer bzw. auch extreme Ausreißer. Ein einfacher Boxplot aus SPSS sieht wie folgt aus:
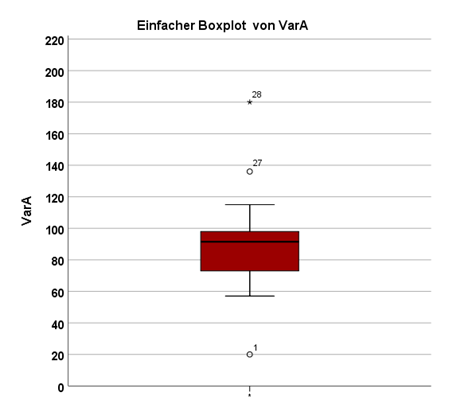
Wir erkennen die eben angesprochenen Elemente und kümmern uns nun um die Interpretation des Boxplots und der jeweiligen Elemente, die er darstellt.
2 Die Box – der Interquartilsabstand
Sollte man einen Boxplot interpretieren müssen, geht es immer mit der Box bzw. dem Kasten los. Sie spannt den Interquartilsabstand (IQA bzw. IQR vom englischen Interquartile range)auf. Dieser ergibt sich aus dem dritten Quartil abzüglich des ersten Quartils. Das dritte Quartil ist der Wert, unter dem 75% der Werte der Verteilung liegen. Das erste Quartil ist entsprechend der Wert, unter dem 25% der Werte liegen. Einen ausführlicheren Artikel zu Quartilen findest du hier. 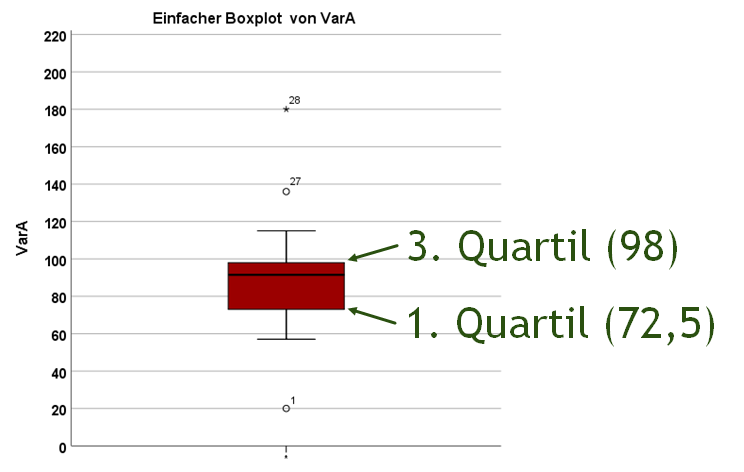
Im Beispiel liegt das dritte Quartil bei 98 und das erste Quartil bei 72,5. Die Differenz drittes Quartil – erstes Quartil ist der sogenannten Interquartilsabstand. Die Box hat also immer die Länge drittes Quartil – erstes Quartil. Im Beispiel wäre sie 25,5 lang (98-72,5).
3 Der Querstrich – der Median
Der Median, auch zweites Quartil genannt, ist ein sehr wichtiger Lageparameter in der Statistik. Er teilt die Verteilung in zwei gleich große Hälften und ist aufgrund dessen und im Gegensatz zum Mittelwert gegenüber Ausreißern nicht anfällig.
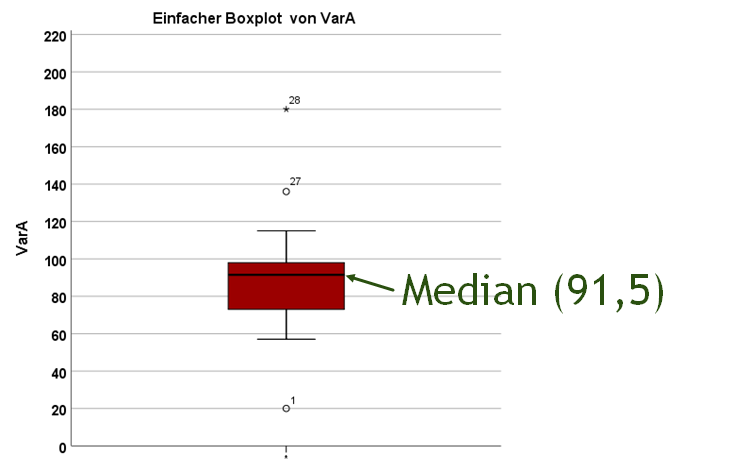
Im Beispiel ist der Median 91,5. Demzufolge sind 50% der Werte der Verteilung kleiner oder gleich diesem Wert und 50% sind größer oder gleich diesem Wert.
4 Antennen – häufig (nicht) die Minimal- und Maximalwerte
Wie bei so vielen Dingen in der Statistik ist es auch mit den Antennen (auch Whisker) nicht ganz so eindeutig. Das liegt an deren Definition. Prinzipiell bilden sie den Minimalwert (untere Antenne) und Maximalwert (obere Antenne) ab. Allerdings ist das nur der Fall, insofern keine einfachen oder extremen Ausreißer in der Verteilung vorliegen, was uns direkt zum nächsten Punkt bringt.
5 Kreise und Sterne – Ausreißer und extreme Ausreißer
5.1 Einfache bzw. milde Ausreißer
Einfache Ausreißer (auch: milde Ausreißer) sind in der Regel so definiert, dass sie mindestens die anderthalbfache Boxlänge (der Interquartilsabstand) von jener Box entfernt sind, Fall 1 und 27: 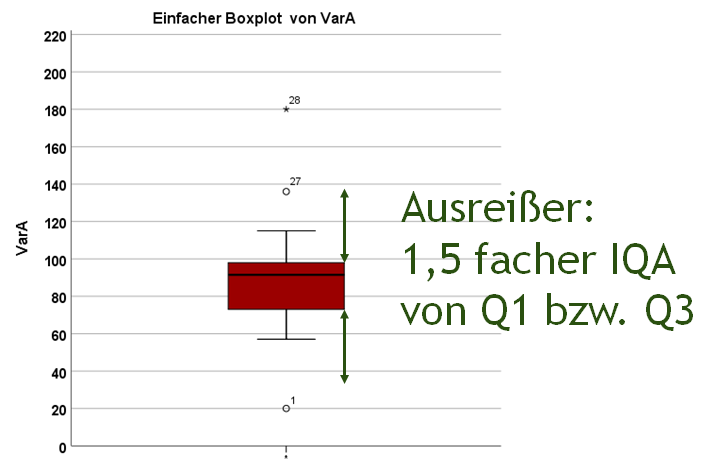
5.2 Extreme Ausreißer
Im Beispiel sind Fall 1 und 27 einfache bzw. milder Ausreißer, weil sie auf oder außerhalb des anderthalbfachen IQA liegen.
Was ist aber mit dem Fall Nr. 28?
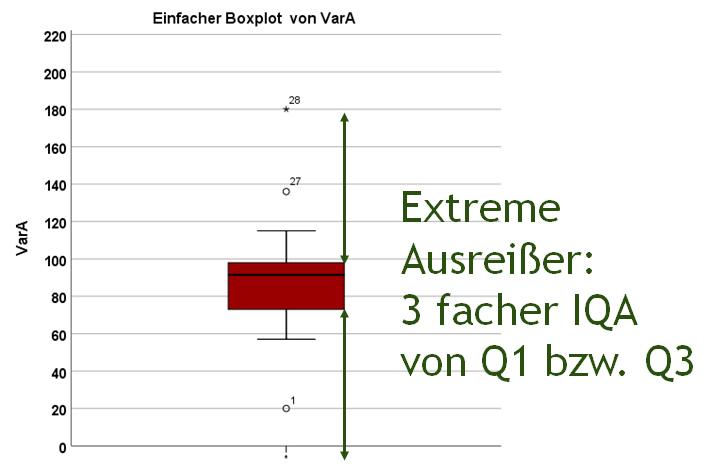
Dieser Fall ist ein extremer Ausreißer, weil er über die dreifache Boxlänge von den jeweiligen Quartilen entfernt sind. Hinweis: in SPSS sind Ausreißer bereits mit 2,5-fachem Interquartilsabstand über bzw. unterhalb der Quartile mit einem * markiert. Eventuell sollte man über einen Ausschluss nachdenken, wie ich in diesem Artikel zeige.
6 Spannweite – die (tatsächlichen) Minimal- und Maximalwerte
Wie wir schon gelernt haben, zeigen die Antennen die Minimal- und Maximalwerte an. Aber nur dann, wenn es keine Ausreißer gibt. Gibt es entsprechend Ausreißer, ist die Spannweite durch die Differenz vom größten und vom kleinsten Ausreißer definiert. Im Beispiel sieht das so aus:
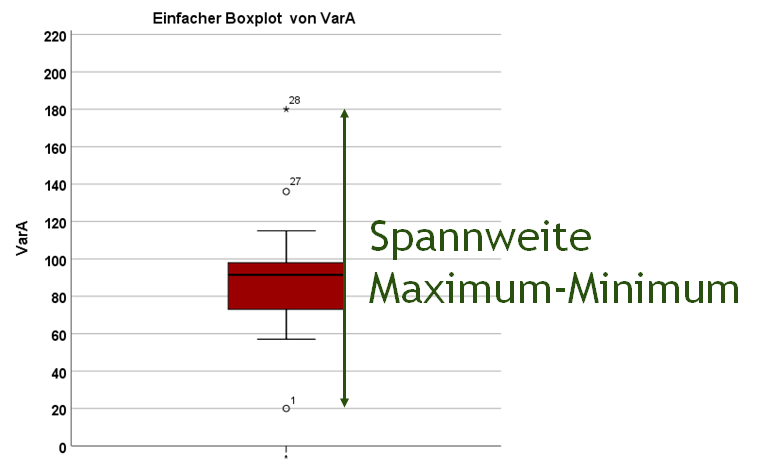
Die Spannweite wäre demzufolge in im Beispiel: 180 (Maximum) – 20 (Minimum) und beträgt 160.
7 Was zeigt ein Boxplot (nicht) – was kann ich beim Boxplot interpretieren?
Wie mittlerweile klar geworden sein sollte, zeigt ein Boxplot:
- Median, 1. Quartil und 3. Quartil
- Ausreißer und extreme Ausreißer
- Streuung (Boxgröße bzw. IQA/IQR)
Anhand dieser Parameter wird man auch den Boxplot interpretieren.
Ein Boxplot zeigt allerdings keine Häufigkeiten. Hierfür ist ein entsprechendes Histogramm heranzuziehen, alternativ ein sog. Violinen-Diagramm. Ein Boxplot zeigt außerdem nicht, ob eine Normalverteilung o.ä. vorliegt.
8 Beispieldaten
Zum Nachvollziehen gibt es hier die von mir verwendete Verteilung. Ihr könnt sie einfach in Excel oder SPSS einfügen und euch ein Boxplot ausgeben lassen. Achtung, in Excel gibt es keine mit * markierten extremen Ausreißer.
20
57
57
57
58
71
72
74
74
81
82
85
89
91
92
93
93
95
96
97
98
98
99
100
104
115
136,26
180
9 Videotutorial


