Inhaltsverzeichnis
1 Boxplot in SPSS erstellen – wie geht das?
Einen Boxplot erstellen – das funktioniert in SPSS recht einfach und mit wenigen Klicks, wie dieser Artikel zeigt. Der Boxplot (auch Kastendiagramm oder Kastengrafik) kombiniert verschiedene Streumaße und inbesondere Lagemaße einer Verteilung und stellt sie grafisch dar.
Einen Boxplot in R erstellen? In diesem Artikel zeige ich euch dies.
Zu Beginn sollten für die Erstellung des Boxplot metrisch skalierte Variablen vorliegen. Aufgrund der verwendeten Lagemaße funktioniert es aber auch mir ordinal skalierten Daten, wenn auch weniger gut, wie ich finde. In einem ersten Schritt ruft ihr die “Diagrammerstellung” in SPSS auf:
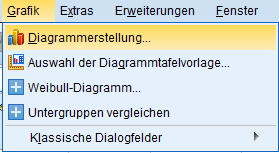
In einem nächsten Schritt bekommt ihr folgendes Dialogfeld angezeigt. Die entsprechende Klickfolge ist unter dem Bild angegeben:
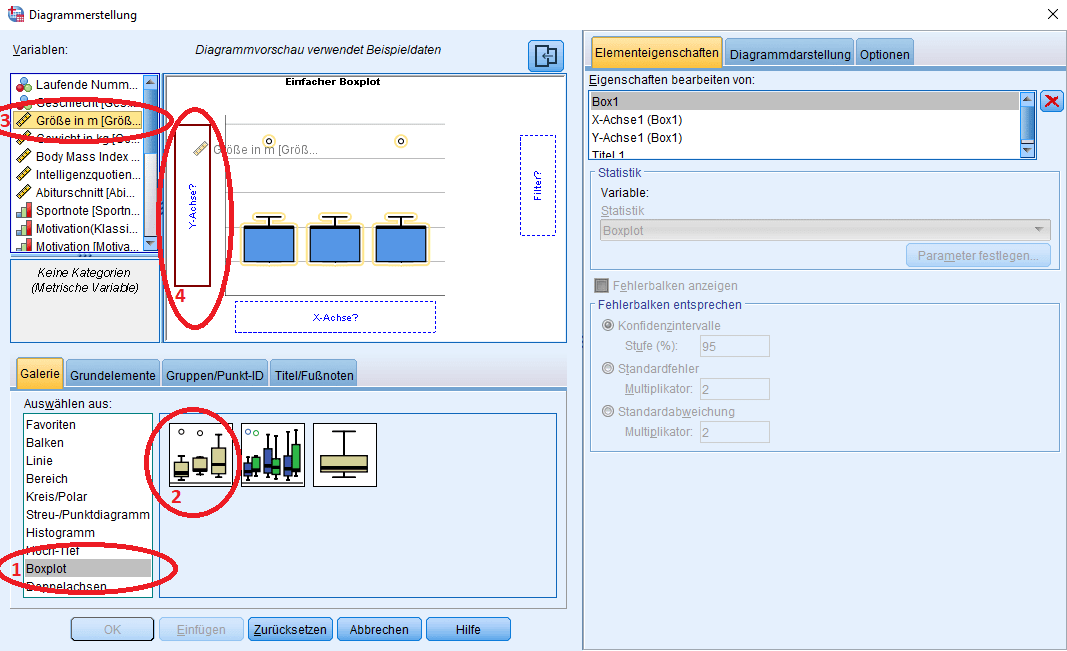
1: Ihr klickt auf Boxplot. Dann erscheinen rechts daneben drei Auswahlmöglichkeiten für Boxplots.
2: Wenn ihr einen einfachen Boxplot erstellen wollt, wählt ihr die linke der drei Möglichkeiten: “einfacher Boxplot”.
3: Als nächstes müsst ihr die darzustellende Variable in eurer Variablenliste raussuchen. Ich habe mich für die Größe in m entschieden.
4: Zum Abschluss zieht ihr die Variable an die Y-Achse im Diagramm. Habt ihr das alles ausgewählt, könnte ihr mit OK den Boxplot erstellen lassen.
2 Den Boxplot von SPSS interpretieren
Der Boxplot aus SPSS unterscheidet sich geringfügig von dem aus Excel oder auch anderen statistischen Auswertungsprogrammen. Eine generelle Auswertungshilfe habe ich in diesem Artikel. Nach ein paar Formatierungen sieht das ganze dann wie folgt aus:
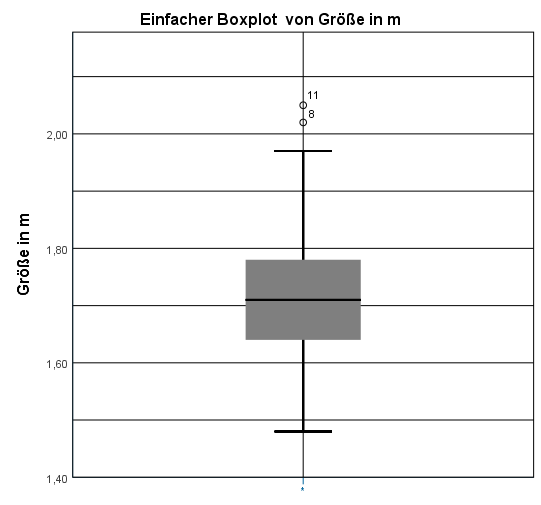
Wie zu erkennen ist, ist es eine recht symmetrische Verteilung. Nun aber zu den einzelnen Bestandteilen.
2.1 Der Median
Der Median ist die horizontale Linie in der Mitte des Kastens und ist die Mitte bzw. das Zentrum der Verteilung. Er liegt im Beispiel bei etwas über 1,70m (analytisch ermittelt: 1,71m). 50% der Fälle haben also einen Größe unter 1,71m und 50% haben eine Größe über 1,71m. Der Median heißt daher auch 50%-Quantil oder 2. Quartil und ist das wichtigste Lagemaß in der Statistik.
2.2 Das 1. Quartil und das 3. Quartil
Das 1. Quartil (25%-Quantil) ist die untere Kante der Box und ist im Beispiel zwischen 1,60m und 1,70m. Anayltisch ermittelt liegt es bei 1,63m. Das heißt, 25% der Fälle haben eine Größe unter 1,63m und 75% der Fälle haben eine Größe über 1,63m. Das 3. Quartil (75%-Quantil) ist analog zu verstehen. Es liegt bei etwas weniger als 1,80m. Analytisch ermittelt sind es 1,78m. Auch hier kann man analog schließen, dass 75% der Fälle eine Größe unter 1,78m haben und 25% eine Größe über 1,78m besitzen.
2.3 Der Interquartilsabstand
Zieht man vom 3. Quartil das 1. Quartil ab, hat man die Höhe des Kastens. 50% der Werte liegen zwischen den beiden Quartilen, also befinden sich im Kasten. Im Beispiel ist dies 1,78m-1,63m und beträgt somit 0,15m. 50% der Fälle unterscheiden sich demnach in ihrer Größe um lediglich 0,15m.
2.4 Antennen
Antennen (auch Whisker) sind bei Boxplots nicht ganz so eindeutig definiert. Prinzipiell bilden sie den Minimumwert (untere Antenne) und Maximalwert (obere Antenne) ab. Im Falle der unteren Antenne stimmt dies im Beispiel und der Wert ist 1,48m. Für die obere Antenne gilt dies nicht, weil noch “Ausreißer” existieren. Faustregel: Existieren einfache oder extreme Ausreißer in der Verteilung, sind die Antennen der Wertebereich, der außerhalb der Box liegt, aber keine Ausreißer darstellen. Das bringt uns direkt zum nächsten Punkt: Ausreißer.
2.5 Kreise und Sterne – Ausreißer und extreme Ausreißer
Ausreißer sind in der Regel so definiert, dass sie bis zur anderthalbfachen Boxlänge (der Interquartilsabstand) von jener Box entfernt sind. im Beispiel sind das zwei Fälle. SPSS bezeichnet die Ausreißer bei Boxplots mit ihrer Fallnummer. Hier sind es also Fall 8 und Fall 11, die bis zum anderthalbfachen Interquartilsabstand von der Box entfernt sind. Schaut man im Datensatz nach diesen beiden Fällen, zeigen sie eine Größe von 2,02m und 2,05m. Extreme Ausreißer gibt es im Beispiel nicht. Sie wären über der anderthalbfache Boxlänge von der Box entfernt. Hinweis: in SPSS sind Ausreißer bereits mit 2,5-fachem Interquartilsabstand über bzw. unterhalb der Quartile mit einem * markiert. Eventuell sollte man über einen Ausschluss nachdenken, wie ich in diesem Artikel zeige.
2.6 Spannweite – die (tatsächlichen) Minimal- und Maximalwerte
Wir wir schon gelernt haben, zeigen die Antennen die Minimal- und Maximalwerte an. Aber nur dann, wenn es keine Ausreißer gibt. Gibt es entsprechend Ausreißer, ist die Spannweite durch die Differenz vom größten und vom kleinsten Wert bzw. Ausreißer definiert.
Die Spannweite wäre demzufolge in im Beispiel: 2,05m (Maximum) – 1,48m (Minimum) und beträgt 0,57m.
2.7 Was zeigt ein Boxplot (nicht) – was kann ich beim Boxplot nicht interpretieren?
Ein Boxplot zeigt keine Häufigkeiten. Hierfür ist ein entsprechendes Histogramm heranzuziehen. Er zeigt außerdem nicht, ob eine Normalverteilung o.ä. vorliegt. Ein kleines Video mit den obigen Erklärungen zum Boxplot interpretieren gibt es auf meinem YouTube-Kanal.
3 Videotutorials
4 Daten
Zum Nachvollziehen gibt es hier die von mir verwendete Verteilung. Ihr könnt sie einfach in Excel oder SPSS einfügen und euch ein Boxplot ausgeben lassen. Achtung in Excel gibt es keine mit * markierten extremen Ausreißer.
| 1,88 |
| 1,74 |
| 1,85 |
| 1,93 |
| 1,67 |
| 1,58 |
| 1,67 |
| 2,02 |
| 1,97 |
| 1,79 |
| 2,05 |
| 1,56 |
| 1,76 |
| 1,73 |
| 1,87 |
| 1,62 |
| 1,72 |
| 1,71 |
| 1,82 |
| 1,89 |
| 1,63 |
| 1,76 |
| 1,57 |
| 1,81 |
| 1,87 |
| 1,78 |
| 1,73 |
| 1,62 |
| 1,54 |
| 1,49 |
| 1,7 |
| 1,71 |
| 1,67 |
| 1,75 |
| 1,6 |
| 1,5 |
| 1,48 |
| 1,67 |
| 1,65 |
| 1,66 |
| 1,78 |
| 1,78 |
| 1,49 |
| 1,65 |
| 1,77 |
| 1,66 |
| 1,74 |
| 1,53 |
| 1,69 |
| 1,66 |
| 1,72 |


