Die binäre logistische Regression ist immer dann zu rechnen, wenn die abhängige Variable nur zwei Ausprägungen hat, also binär bzw. dichotom ist. Es wird dann die Wahrscheinlichkeit des Eintritts bei Ändern der unabhängigen Variable geschätzt. Die Schätzung der Wahrscheinlichkeit ist neben der binären Codierung der wesentliche Unterschied zur einfachen Regression.
Im Vorfeld der Regressionsanalyse kann zudem eine Filterung vorgenommen werden, um nur einen gewissen Teil der Stichprobe zu untersuchen, bei dem man am ehesten einen Effekt erwartet. Ist die abhängige Variable metrisch oder quasi-metrisch, kann eine lineare Regression (einfach oder multipel) gerechnet werden. Für die Interpretation eines metrischen Prädiktors findet ihr hier mehr Information.
Inhaltsverzeichnis
1 Voraussetzungen der binär logistischen Regression
Die wichtigsten Voraussetzungen sind:
- die y-Variable ist binär codiert (0 und 1 als Ausprägungen), ist sie metrisch, ist eine einfache oder multiple lineare Regression zu rechnen
- metrisch skalierte x-Variable(n), ordinal funktioniert auch, nominal skalierte x-Variablen sind als “kategorial” zu definieren
- keine hoch korrelierten x-Variablen
2 Durchführung der binär logistischen Regression in SPSS
Das von mir gewählte Beispiel versucht die Wahrscheinlichkeit eines Produktkaufes mit der Produktfarbe zu erklären. Die abhängige (y-)Variable ist also das der Kauf eines Produktes (0 – nein und 1 – ja). Das ist wichtig und die Grundlage zum Verstehen der nachfolgenden Ausführungen. Die unabhängige (x-)Variable ist die Produktfarbe. Es existiert also nur eine kategorial skalierte x-Variable. Sie hat folgende Ausprägungen: 0-bunt, 1-weiß, 2-schwarz.
Über das Menü in SPSS: Analysieren -> Regression -> Binär logistisch
Als abhängige Variable ist die binär codierte Variable einzutragen. In meinem Falle “Führerschein beim 1. Versuch”. Die x-Variable “IQ” gehört in das Feld “Kovariaten“. Kovariate und x-Variablen sind synonym zu sehen. Als Methode ist “Einschluss” zu wählen.
Es gibt Autoren, die empfehlen hier schrittweise – bei nur einem Prädiktor wie in diesem Beispiel ist das Ergebnis jedoch identisch. HINWEIS: Sofern es sich nicht um ein exploratives Vorgehen handelt und explizit Hypothesen theoretisch fundiert hergeleitet wurden, ist stets Einschluss zu wählen.
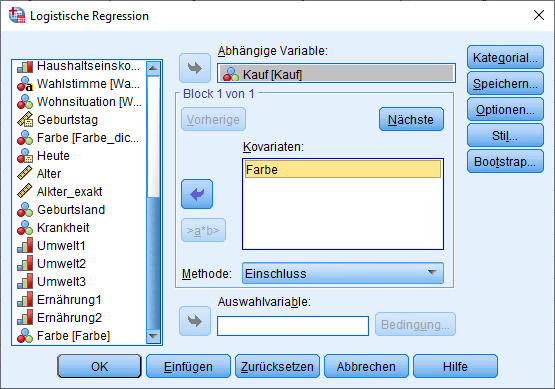
Als nächstes ist es notwendig, festzulegen, dass Farbe kategorial skaliert ist und auch innerhalb der Regression als solche behandelt werden soll. Hierzu ist über den Button Kategorial folgendes Menü aufzurufen. Die kategoriale Kovariate ist als solche zu definieren, indem man sie in das rechte Feld verschiebt. Als Kontrast kann “Indikator” stehen bleiben. Lediglich bei der Referenzkategorie kann man wählen. Hier besteht die Möglichkeit “Letzte” und “Erste” zu wählen. Standardmäßig ist “Letzte” selektiert. Im Beispiel wäre das die Ausprägung 2 (Farbe schwarz). Für die folgenden Ausführungen lasse ich als Referenzkategorie “Letzte” (Ausprägung 0), weil ich die Wirkung eines schwarzen Produktes gegen ein jeweils buntes und weißes Produkt auf die Kaufwahrscheinlichkeit testen möchte.
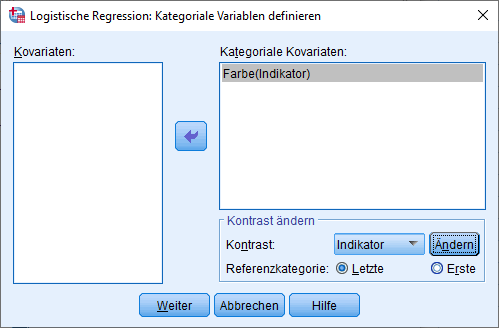
Danach noch ein Klick auf Optionen. Hier sind auszuwählen:
- “Klassifikationsdiagramme“
- “Hosmer-Lemeshow-Anpassungsstatistik” und
- “Konfidenzintervall für Exp(B) 95“

Danach ein Klick auf Weiter und dann auf OK zur Berechnung. Im nächsten Schritt geht es um die Interpretation der erhaltenen Ergebnisse der binär logistischen Regression.
3 Interpretation der Ergebnisse der binär logistischen Regression in SPSS
Im Gegensatz zur linearen Regression ist die Interpretation der Ergebnisse der binär logistischen Regression etwas umfangreicher.
3.1 Der Anfangsblock – kurze Kontrolle
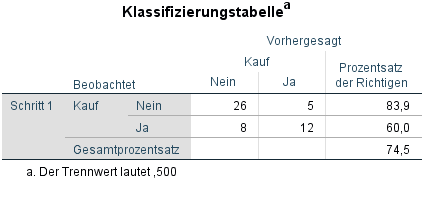
Der Anfangsblock bzw. Block 0 ist so gut wie immer unwichtig. Hier wird das Modell ohne kategoriale unabhängige Variable geschätzt. Das erkennt man daran, dass in der Tabelle “Variablen in der Gleichung” lediglich die Konstante steht. In der Tabelle “Variablen nicht in der Gleichung” ist die Farbe mitsamt ihren Ausprägungen zu sehen – samt Signifikanz. In der “Klassifizierungstabelle” kann man zudem erkennen, dass für alle 51 Fälle (31+20) die Vorhersage nein ist. Das Modell sagt also vorher, dass ein Kauf nicht erfolgt.
Der Prozentsatz der Richtigen zeigt entsprechend 100 in der ersten Zeile (jene Fälle, wo tatsächlich kein Kauf stattgefunden hat) und 0 in der zweiten Zeile (jene Fälle, wo tatsächlich ein Kauf stattfand). Im Ergebnis wurden zumindest 60,8 % der Fälle richtig vorhergesagt – das liegt natürlich an den 31 richtigen (nein-)Fällen.
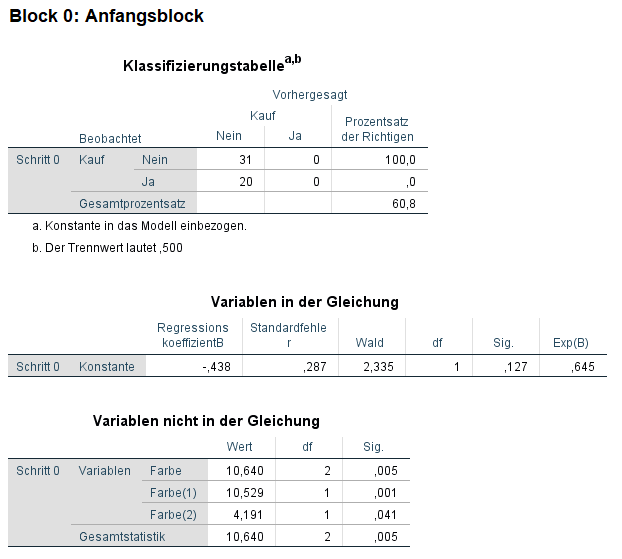
3.2 Der Block 1 – Interpretationsbedarf
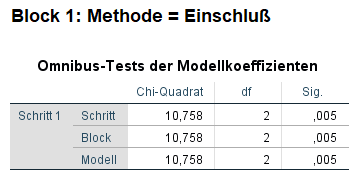
Im Block 1 ist zunächst die Omnibus-Test der Modellkoeffizienten von Interesse. Der Test ist ein Likelihood-Quotient-Chi-Quadrat-Test. Er vergleicht das aktuelle Modell (Block 1) mit dem Nullmodell (Anfangsblock/Block 0). Der Signifikanzwert ist bei der Methode Einschluss in der Zeile Modell abzulesen und ist 0,005. Er liegt damit unter der typischen Verwerfungsgrenze von 0,05 und zeigt an, dass das aktuelle Modell mit Einbezug der Produktfarbe besser geeignet ist als das Nullmodell – ohne jegliche unabhängige Variablen.
Die Modellgüte wird in der Tabelle “Modellzusammenfassung” aufgezeigt. Ein kleiner -2LogLikelihood-Term ist ein Zeichen für ein höheres R². Ein höheres R² steht für eine bessere Modellpassung. Das R² ist allerdings nur ein Pseudo-R², damit analog zum R² der linearen Regression eine Interpretation der Güte vorgenommen werden kann.
Cox & Snell R² ist stets kleiner als Nagelkerkes R², weil die Wertebereiche unterschiedlich sind. Cox & Snell R² kann als Höchstwert 0,75 haben. Nagelkerkes ist eine Standardisierung von Cox & Snell und hat damit einen Höchtswert von 1 – analog zum R² der linearen Regression. Im Beispiel ist Cox & Snell R² 0,190 und Nagelkerkes R² beträgt 0,258.
Diese Werte sind – je nach Forschungsbereich – als niedrig oder mittel anzusehen. Da es sich um ein konstruiertes Beispiel handelt, kann per se keine Qualitätsaussage getroffen werden.

Als nächstes folgt der Hosmer-Lemeshow-Test. Er gibt an, wie stark die beobachteten und vorhergesagten Fälle voneinander abweichen ( = Fit). Hier sollte die Signifikanz nicht unter 0,05 liegen, da dies einen schlecht Fit zur Folge hätte. Die Nullhypothese geht von ungefährer Gleichheit der beobachteten und vorhergesagten Fälle aus, daher sollte sie nicht verworfen werden, die Signifikanz also über 0,05 liegen. Im Beispiel liegt die Signifikanz bei 1 und damit ist alles in Ordnung.

Da es eben schon um beobachtete und vorhergesagte Fälle ging, kann dies in der Klassifizierungstabelle noch mal im Detail betrachtet werden. Im Block 0 hatten wir ja auch eine solche Tabelle, die für alle Fälle einen Nichtkauf des Produktes vorhergesagt hatte.
Nun haben wir unter Einschluss der unabhängigen Variable Farbe eine neue Klassifizierungstabelle. Hier interessiert uns vor allem die Diagonale von links oben nach rechts unten. Hier entsprechen sich die beobachteten und vorhergesagten Fälle. Das Modell sagt 26 mal korrekt den NICHTkauf und 12 mal korrekt den Kauf vorher. In 5 Fällen prognostiziert das Modell einen Kauf, obwohl das Produkt nicht gekauft wurde. In 8 Fällen wurde durch das Modell kein Kauf vorhergesagt, obwohl es tatsächlich einen Kauf gab.
Die Prozentsätze der Richtigen sind mit insgesamt 74,5% schon recht gut. Daumenregeln, was gut ist, gibt es hier nicht unbedingt. Bei 50% kann man salopp gesagt – zumindest bei ähnlich großen Gruppen – auch eine Münze werfen und braucht kein Modell bemühen. 60%-70% sollten es demnach schon sein.
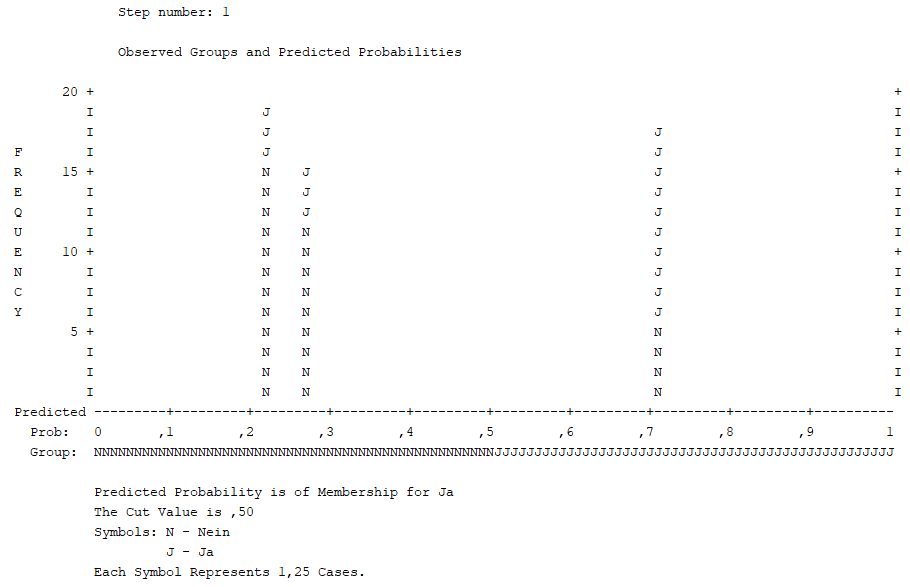
Die richtige Zuordnung kann man auch im Klassifikationsdiagramm sehen. Unter dem Diagramm gibt es die Zeile “Group“. Dies sind die vorhergesagten Gruppenzuordnungen, also ob ein Kauf erfolgte oder nicht.
Ein “j” steht dabei für einen Kauf, ein “n” für keinen Kauf. Man kann bei 0,7 in der “Gruppe j” ein paar “n” erkennen. In der letzten Zeile unter dem Diagramm steht “Each Symbol Represents 1,25 Cases“. Das heißt, ein “n” steht für 1,25 Fälle – ACHTUNG: dies schwankt erheblich mit eurer Stichprobengröße! In der “Gruppe j” sind insgesamt vier “n” zu sehen, also umgerechnet 5 Fälle. Das bedeutet, 5 Fälle, die tatsächlich keinen Kauf tätigten, wurden fälschlicherweise mit Kauf prognostiziert.
Das haben wir auch oben in der Klassifizierungstabelle ablesen können. Das Klassifikationsdiagramm in der binär logistischen Regression ist also einfach noch mal eine grafische Darstellung der Klassifizierungstabelle. Zusätzlich sieht man die Wahrscheinlichkeit der Zuordnung in der Zeile “Prob” unter dem Diagramm. Hier sollten im Ideallfall viele Fälle an den Seiten stehen, weil dies für eine höhere Wahrscheinlichkeit/Sicherheit der Zuordnung steht.
Schließlich ist die Koeffiziententabelle zu interpretieren. Hier sieht man die Konstante und die Farben. Die Konstante ist nicht wichtig und wir konzentrieren uns lediglich auf die unabhängigen Variablen, hier die Farbe. Ursprünglich existierten 3 Kategorien für die unabhängige Variable Farbe (0-bunt, 1-weiß, 2-schwarz). Da ich oben schwarz als Referenzkategorie ausgewählt habe, erscheint diese nicht als Koeffizient in der Tabelle.
Die angezeigten Koeffizienten für bunt (Farbe(1)) und weiß (Farbe(2)) sind nun im Vergleich zur Referenzkategorie (Farbe schwarz) zu verstehen. Bunt (Farbe(1)) unterscheidet sich signifikant von der Referenzkategorie schwarz. (p=0,017) und hat einen Regressionskoeffizient B von 1,887 und ist damit positiv. Das bedeutet zunächst, dass die Wahrscheinlichkeit eines Kaufes des Produktes steigt, wenn das Produkt bunt ist (Referenzkateogrie schwarz). Da auch das 95% Konfidenzintervall angegeben wurde, kann dies auch herangezogen werden. Hier sollte für eine Signifikanz der Wert 1 nicht im Intervall eingeschlossen sein, also beide Werte entweder über oder unter 1 liegen.
Weiß (Farbe (2)) hat eine geringere Wahrscheinlichkeit für einen Kauf als die Referenzkategorie schwarz. Der Regressionskoeffizient ist negativ. Allerdings unterscheidet sich weiß, verglichen mit bunt in seiner Wirkung auf den Kauf allerdings nicht signifikant von der Referenzkategorie schwarz (p=0,702).
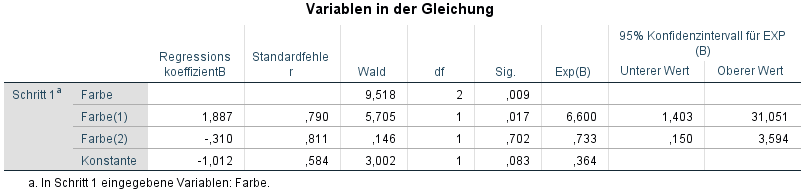
Als nächstes schaut man sich das Odd’s ratio an, was bei SPSS im Rahmen der binär logistischen Regression unter Exp(B) steht:
- Exp(B) kann aus B ermittelt werden: e^B = Exp(B), also e^1,887 = 6,600.
- Exp(B) > 1 bedeutet eine “positiven Einfluss” auf die abhängige Variable.
- Ist Exp(B) < 1, ist es ein negativer Einfluss der abhängigen Variable.
- Bei Exp(B) = 1 ändert sich nichts.
Exp(B) korrespondiert mit dem Regressionskoeffizienten. Ist Exp(B) > 1, ist der Regressionskoeffizient positiv und vice versa. Im konkreten Beispiel ist Exp(B) = 6,600 – was zum positiven Koeffizient von 1,887 passt – und somit wird ein buntes Produkt (Farbe(1)) wahrscheinlicher gekauft als ein schwarzes Produkt (Farbe (0)).
Die Wahrscheinlichkeit eines Produktkaufes ist also 6,6 mal höher, wenn das Produkt bunt statt schwarz ist.
Schließlich kann man noch folgendes Berechnen: Zieht man vom Odd’s ratio einer unabhängigen Variable 1 ab, erhält man die Wahrscheinlichkeit der Gruppenzugehörigkeit (= Kauf) beim Wechsel von der Produktfarbe schwarz (Farbe 0) zu bunt (Farbe 2).
Konkret heißt das: Das odd’s ratio für die Farbe (1) ist 6,6. Zieht man hiervon 1 ab (6,6-1), erhält man 5,6. Dies sind 560%. Die relative Wahrscheinlichkeit eines Kaufes steigt demnach um 560%, wenn das Produkt schwarz ist, verglichen mit bunt.
4 Tipp zum Schluss
Findest du die Tabellen von SPSS hässlich? Dann schau dir mal an, wie man mit wenigen Klicks die Tabellen in SPSS im APA-Standard ausgeben lassen kann.
5 Videotutorial


