Inhaltsverzeichnis
1 Ziel der zweifaktoriellen Varianzanalyse (ANOVA)
Die zweifaktorielle Varianzanalyse (kurz: ANOVA) testet unabhängige Stichproben darauf, ob bei mehr als zwei unabhängigen Stichproben die Mittelwerte unterschiedlich sind. Im Unterschied zur einfaktoriellen Varianzanalyse gibt es bei der zweifaktoriellen Varianzanalyse zwei unabhängige Variablen (Faktoren), die einen Einfluss auf eine unabhängige Variable haben. Die Varianzanalyse in SPSS kann man mittels weniger Klicks durchführen, wie nachfolgend erkennbar ist.
2 Voraussetzungen für die zweifaktorielle Varianzanalyse (ANOVA)
Die wichtigsten Voraussetzungen sind:
- mehr als zwei voneinander unabhängige Stichproben/Gruppen
- metrisch skalierte y-Variable
- nominal/ordinal skalierte unabhängige Variablen (Faktoren)
- normalverteilte Fehlerterme innerhalb der Gruppen
- Homogene (nahezu gleiche) Varianzen der y-Variablen der Gruppen (Levene-Test über die Ausgabe beim Durchführen der ANOVA)
- Optional: fehlende Werte definiere, fehlende Werte identifizieren und fehlende Werte ersetzen
Fragen können unter dem verlinkten Video gerne auf YouTube gestellt werden.
3 Durchführung der zweifaktoriellen Varianzanalyse (ANOVA) in SPSS
Über das Menü in SPSS:
Analysieren > Allgemeines lineares Modell > Univariat
1. Als Faktorensind die Gruppentrennenden Merkmale/Variablen auszuwählen. Im Beispiel habe ich Pflanzen, die in unterschiedlich beheizten Gewächshäusern stehen und zudem unterschiedlich gedüngt werden und beobachte deren Wachstum.

2. Unter Optionen Deskriptive Statistiken, Homogenitätstests und Schätzungen der Effektgröße auswählen sowie ein Interaktionsterm aus den beiden Faktoren in den Bereich “Mittelwerte anzeigen für” einfügen.

3. Bei Diagramme den Faktor als Horizontale Achse definieren und auf hinzufügen klicken.

4. Unter Post hoc den oder die gewünschten Faktoren als “Post-hoc Tests für” auswählen und “Bonferroni” anhaken – dient dem mehrfachen paarweisen Vergleich zwischen den durch die Faktoren definierten Gruppen.

4 Interpretation der Ergebnisse für die zweifaktorielle Varianzanalyse in SPSS (ANOVA)
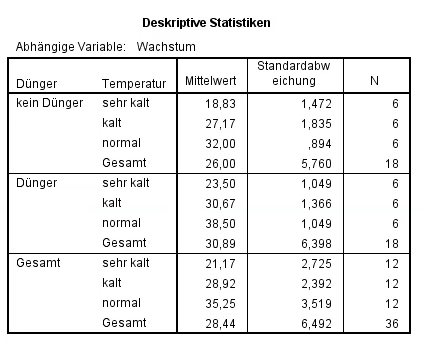
0. Ein deskriptiver Überblick ist ein guter Start und hilft bei der späteren Interpretation. Hier ist erkennbar, dass zunächst der erste Faktor (kein Dünger/Dünger) und dann unterteilt danach 3 Temperaturstufen (sehr kalt/kalt/Normal) aufgelistet werden. Erwartungsgemäß ist die Pflanzengruppe, die gedüngt und unter normalen Temperaturen wachsen konnte, am stärksten gewachsen. Weitere Schlüsse lassen sich erst in detaillierten Auswertungen vornehmen.
Ganz unten im Output findet man zusätzlich das Profildiagramm, dass dies noch mal grafisch veranschaulicht:

1. Die Voraussetzung der Varianzhomogenität wird mit dem Levene-Test direkt mit den Ergebnissen der zweifaktoriellen Varianzanalyse (ANOVA) ausgegeben. Die Nullhypothese lautet hierbei, dass die Varianzen homogen sind. Die Signifikanz sollte demzufolge über 0,05 liegen, damit sie nicht verworfen werden kann und den Stichproben homogene Varianzen bescheinigt werden. Hier ist p=0,333 und die Nullhypothese von Varianzhomogenität kann nicht verworfen werden. Es liegen als in etwa gleiche Varianzen vor.

2. Die Tabelle “Tests der Zwischensubjekteffekte” zeigt, ob die Faktoren einen Haupteffekt haben. Das erkennt man in der Zeile, in der die vorher definierten Faktoren stehen. Ist die Signifikanz kleiner als 0,05, geht man von statistisch signifikanten Unterschieden aufgrund des jeweiligen Faktors hinsichtlich der Mittelwerte zwischen den Stichproben aus. Ist der Interaktionseffekt (Faktor1*Faktor2) jedoch signifikant, hängt ein Teil des Effektes des einen vom anderen Faktor ab. Dies ist im Vorfeld des Testes entsprechend zu begründen. In diesem Fall werden die Haupteffekte NICHT interpretiert. Ist der Interaktionseffekt nicht signifikant, werden entsprechend die Haupteffekte interpretiert.
Im Beispiel ist der Interaktionseffekt aus Dünger*Temperatur statistisch signifikant (p=0,03). Somit ist eine Interpretation der Haupteffekte (nur Dünger und nur Temperatur) unnötig, da gerade deren Zusammenspiel das Pflanzenwachstum statistisch signifikant beeinflusst. Oder anders gesprochen, der eine Faktor verstärkt im Beispiel die Wirkung des anderen Faktors – dies sollte im Vorfeld ebenfalls klar sein.

3. ACHTUNG: Ein 1-seitiges Testen ist nicht möglich, da bei mehr als zwei Gruppen nicht gesagt werden kann, welche Gruppe einen größeren oder kleineren Wert hat.
4. In der Tabelle “Mehrfachvergleiche” sieht man die paarweisen Vergleiche, die sog. post hoc-Tests – das sind lediglich unabhängige t-Tests für alle möglichen Kombinationen der Faktoren. Sie lassen erkennen, auf welchen Faktorstufen signifikante Unterschiede zustande kommen und sind sehr aufschlussreich und unbedingt an die ANOVA anzuschließen. Hier wird in der ersten Spalte eine Gruppe und in der zweiten Spalte paarweise mit allen anderen Gruppen getestet. Auch hier ist das Hauptaugenmerk auf die Signifikanz zu richten. Wenn zwischen zwei Gruppen ein statistisch signifikanter Unterschied besteht, ist auch hier der Signifikanzwert kleiner als 0,05.
Im Beispiel habe ich nur für die Temperatur post-hoc-Tests angefordert (siehe oben). Neben Bonferroni sieht man noch Tukey-HSD als Korrektur für den kumulierten Alphafehler . Kumulierter Alphafehler bedeutet, dass bei mehrfachem anayltischen Test mit denselben Gruppen der Alphafehler (Fälschliches Ablehnen der Nullhypothese keines Effektes) unweigerlich steigt. Um also zu verhindern, dass man Effekte diagnostiziert, die nicht vorhanden sind, muss der p-Wert korrigiert werden. Im Beispiel sind alle Unterschiede signifikant – ein in der realen Welt eher nicht vorkommendes Phänomen.
Da ich aber bereits in 2. festgestellt habe, dass ich eine signifikante Interaktion habe, ist eine Analyse der post-hoc-Tests nicht zwingend notwendig. Hat man signifikante Haupteffekte, fordert man für jene die post-Hoc-Analyse an.
5. Die Effektstärke wird von SPSS nicht ausgegeben, also wie stark sich die Stichproben unterscheiden. Die ist manuell zu berechnen und mit Cohen: Statistical Power Analysis for the Behavioral Sciences (1988), S. 284-287 zu beurteilen. Die Berechnung erfolgt über die Formel mit f als Wurzel aus Eta² geteilt durch Eta²+1.

Ab 0,1 ist es demnach ein schwacher Effekt, ab 0,25 ein mittlerer und ab 0,4 ein starker Effekt.
5 Videotutorials
Weitere nützliche Tutorials findest du auf meinem YouTube-Kanal.


