Inhaltsverzeichnis
1 Ziel der einfaktoriellen Varianzanalyse (ANOVA)
Die einfaktorielle Varianzanalyse (kurz: ANOVA) testet unabhängige Stichproben darauf, ob bei mehr als zwei unabhängigen Stichproben die Mittelwerte unterschiedlich sind. Die Nullhypothese lautet, dass keine Unterschiede (hinsichtlich der zu untersuchenden Variable) existieren. Demzufolge lautet die Alternativhypothese, dass zwischen den Gruppen Unterschiede existieren. Es ist also das Ziel, die Nullhypothese zu verwerfen und die Alternativhypothese anzunehmen. Die Varianzanalyse in Excel kann man mittels weniger Klicks durchführen. In SPSS und R kann man sie auch rechnen. Ein kurzes Tutorial zur zweifaktoriellen Varianzanalyse ist hier zu finden.
2 Voraussetzungen der einfaktoriellen Varianzanalyse (ANOVA)
Die wichtigsten Voraussetzungen sind:
- mehr als zwei voneinander unabhängige Stichproben/Gruppen
- metrisch skalierte y-Variable
- normalverteilte Fehlerterme innerhalb der Gruppen
- Homogene (nahezu gleiche) Varianzen der y-Variablen der Gruppen (Levene-Test über die Ausgabe beim Durchführen der ANOVA)
3 Durchführung der einfaktoriellen Varianzanalyse in Excel (ANOVA)
Über das Menü in Excel: Reiter “Daten” > “Datenanalyse” > “Anova: Einfaktorielle Varianzanalyse”

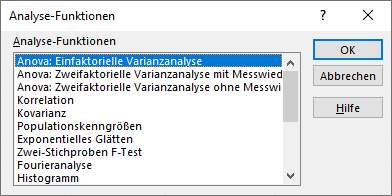
Hinweis: Sollte die Funktion “Datenanalyse” nicht vorhanden sein, ist diese über “Datei” > “Optionen” > “Add-Ins” > “Verwalten” > “Los…” zu aktivieren. Dieses Video zeigt dies kurz.
1. Als Eingabebereich muss mann die betreffenden Daten auswählen. Wenn die Gruppen nebeneinander stehen, ist bei “Geordnet nach” Spalten auszuwählen. Wenn die Gruppen untereinander stehen, muss man Zeilen auswählen. Damit ist für Excel klar, wie die Daten strukturiert sind.
Achtung: Zwischen den Gruppen dürfen keine Leerzellen exisiteren!
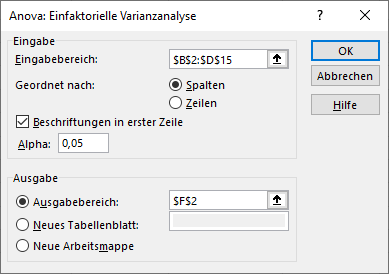
2. Je nachdem, ob in der ersten Zeile eine Beschriftung existiert, die im Eingabebereich mit markiert wurde, ist der Haken zu setzen.
3. Das Alpha von 0,05 ist die typische Irrtumswahrscheinlichkeit. Je niedriger es gewählt wird, desto geringer ist die Wahrscheinlichkeit einen Fehler 1. Art zu begehen. Ein Fehler 1. Art ist das fälschliche Ablehnen der Nullhypothese (= es existieren keine Gruppenunterschiede) zugunsten der Alternativhypothese (= es existieren Gruppenunterschiede). Da man die Alternativhypothese versucht anzunehmen, sollte die Wahrscheinlichkeit einer fälschlichen Annahme so gering wie möglich sein. 0,05 hat sich in der Statistik diesbezüglich als hinreichend erwiesen. Je nach Fachbereich kann der typische Wert aber kleiner (z.B. 0,01) sein.
3. Als Ausgabe kann man mit Ausgabebereich einen Bereich im aktuellen Tabellenblatt wählen. Neues Tabellenblatt und Neue Arbeitsmappe stehen ebenfalls zur Verfügung.
4 Interpretation der einfaktoriellen Varianzanalyse in Excel (ANOVA)
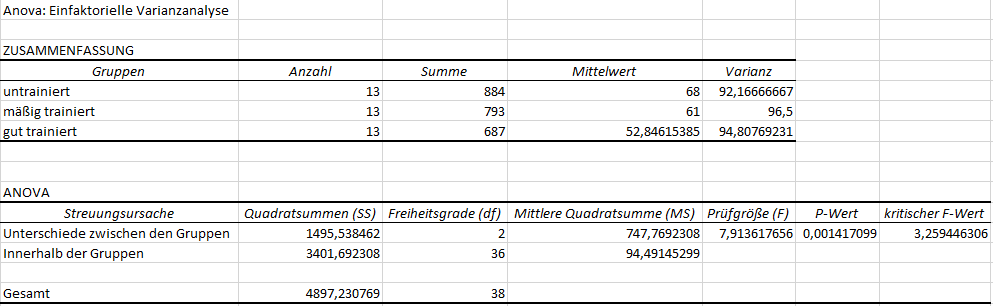
1. Die Voraussetzung der Varianzhomogenität kann man ganz gut in der Tabelle ZUSAMMENFASSUNG erkennen. Die Varianzen der drei Gruppen “untrainiert”, “mäßig trainiert” und “gut trainiert” sind recht ähnlich, sodass die Voraussetzung als erfüllt gelten kann. Wer einen Test rechnen muss/möchte, schaut sich den Levene-Test an. Ist ungefähre Varianzgleichheit nicht erfüllt, muss man einen Kruskal-Wallis-Test rechnen.
2. Die Tabelle ANOVA zeigt, ob statistisch signifikante Unterschiede hinsichtlich der Gruppen existieren. Das erkennt man in der Spalte p-Wert daran, ob dieser unter 0,05 bzw. dem vorher festgelegten Alpha liegt. Im obigen Fall ist p=0,00142 und damit kleiner als 0,05. Die Nullhypothese von Gleichheit zwischen den Gruppen kann demnach verworfen werden. Demzufolge wird die Alternativhypothese von Ungleichheit angenommen. Das kann man auch an der Prüfgröße (F) erkennen. Sie ist 7,914 und liegt über dem kritischen F-Wert von 3,259. Liegt der Prüfwert über dem kritischen Wert, wird ebenfalls die Nullhypothese abgelehnt. Es ist auch in der Tabelle ZUSAMMENFASSUNG erkennbar, dass der Mittelwert und auch die Summe der Werte in den Gruppen bei der Zugehörigkeit zu einer intensiveren Trainingsgruppe sinkt.
3. ACHTUNG: Ein 1-seitiges Testen ist nicht möglich, da bei mehr als zwei Gruppen nicht gesagt werden kann, welche Gruppe einen größeren oder kleineren Wert hat.
4. Es ist allerdings nicht erkennbar, welche der Gruppenunterschiede dafür verantwortlich ist, dass die Nullhypothese von Gleichheit verworfen wird. Hierzu bedarf eines post-hoc-Tests, der in Excel allerdings nicht implementiert ist. Man behilft sich hier mit t-Tests bei unabhängigen Stichproben (auch: Zweistichproben t-Test).
5. Die Effektstärke f wird von Excel nicht ausgegeben, also wie stark sich die Gruppen unterscheiden. Hierzu wird typischerweise f verwendet und mit Cohen: Statistical Power Analysis for the Behavioral Sciences (1988), S. 284-287 beurteilt. Allerdings interessiert uns eher die Größe des Effektes jener Gruppen, die sich voneinander unterscheiden, was ich im Rahmen der post-hoc-Analyse zeige.
5 Post-Hoc-Tests
5.1 t-Tests als Post-Hoc-Tests
Wie ein t-Test für unabhängige Stichproben im Detail funktioniert, habe ich hier gezeigt, weswegen ich an dieser Stelle lediglich die Ergebnistabellen zeige.
WICHTIG: Es müssen alle Gruppen jeweils mit den anderen verglichen werden.
- Bei 3 Gruppen: 1-2, 2-3 und 1-3
- Bei 4 Gruppen: 1-2, 2-3, 3-4, 1-3, 2-4 und 1-4
Im Beispiel habe ich 3 t-Tests gerechnet: 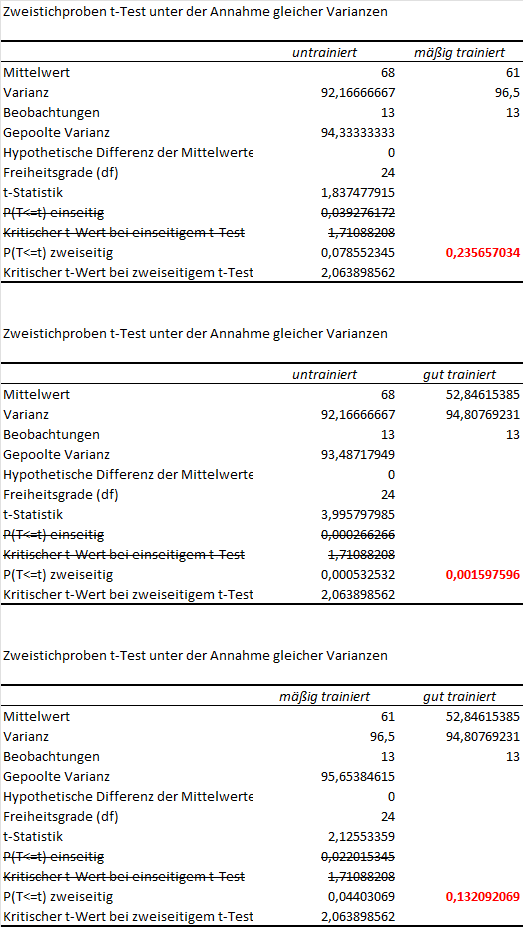
- Es ist ZWINGEND eine Alphafehlerkorrektur durchzuführen. Der Alphafehler (= Fehler 1. Art, siehe auch oben) steigt bei mehrfachem Testen mit denselben Gruppen.
- Eine sehr konservative und zugleich einfache Möglichkeit ist die sog. Bonferroni-Korrektur. Hierbei wird der aus dem t-Test erhaltene p-Wert mit der Anzahl der paarweisen Vergleiche multipliziert.
- Dieser korrigierte p-Wert ist dann wie gewohnt zu interpretieren.
- Im Beispiel habe ich in Excel die p-Werte mit 3 multipliziert, da ich 3 Tests rechnen musste. Der korrigierte p-Wert ist jeweils in rot und fett hervorgehoben.
- Wie zu erkennen ist, ist nur einer der korrigierten p-Werte unter der Grenze von 0,05: untrainiert vs. gut trainiert (p=0,0016). Folglich besteht nur zwischen diesen beiden Gruppen ein Unterschied. Schließlich ist dieser Unterschied noch mit der Effektstärke Cohen’s d zu quantifizieren.
5.2 Effektstärke der post-hoc-Tests
![]()
![Rendered by QuickLaTeX.com \[s = \sqrt{\frac{(n_{1}-1)\cdot s_{1}^{2} + (n_{2}-1)\cdot s_{2}^{2}} {n_{1}+n_{2}-2}} \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-caf462eff0873927a026ce8f5d42c09f_l3.png)
![]()
Im Beispiel sind die Mittelwerte 61 und 52,38 (siehe oben) sowie die gepoolte Standardabweichung 9,85. Eingesetzt in die obige Formel:
![]()
- ab 0,2 klein,
- ab 0,5 mittel und
- ab 0,8 stark.
ACHTUNG: Je nach Disziplin können andere Grenzen gelten. Dies ist im Vorfeld zu prüfen.
6 Videotutorial
Weitere nützliche Tutorials findest du auf meinem YouTube-Kanal.


