Inhaltsverzeichnis
1 Ziel der Varianzanalyse mit Kovariaten (ANCOVA)
Die Varianzanalyse mit Kovariaten (kurz: ANCOVA) testet, wie auch die ANOVA, unabhängige Stichproben darauf, ob bei mehr als zwei unabhängigen Stichproben die Mittelwerte einer abhängigen Variable unterschiedlich sind. Allerdings prüft sie zusätzlich einen weiteren sehr wahrscheinlichen Einflussfaktor (die Kovariate) mit. Die ANCOVA kann in SPSS mit wenigen Klicks durchgeführt werden. Dies zeige ich genauso, wie die wichtige Interpretation der Ergebnisse.
2 Voraussetzungen der Varianzanalyse mit Kovariaten (ANCOVA)
Die wichtigsten Voraussetzungen sind:
- metrisch skalierte y-Variable
- normalverteilte Fehlerterme innerhalb der Gruppen bzw. generell im Modell
- Homogene (nahezu gleiche) Varianzen der y-Variablen der Gruppen (Levene-Test über die Ausgabe beim Durchführen der ANCOVA)
- Kovariate sollten über Gruppen hinweg ähnlich/homogen sein
- Homogenität der Regressionssteigungen
- Optional: fehlende Werte definiere, fehlende Werte identifizieren und fehlende Werte ersetzen
Fragen können unter dem verlinkten Video gerne auf YouTube gestellt werden.
3 Ein Beispiel einer ANCOVA
Wir testen Probanden und deren Ruhepuls. Allerdings sind die Probanden in verschiedene Gruppen eingeteilt, eine untrainierte und eine trainierte Gruppe. Wir kontrollieren aber zusätzlich noch für die Motivation der Probanden. Konkret unterstellten wir: Probanden, die trainierter sind, haben einen niedrigeren Ruhepuls. Hierbei wird für den potentiellen Einfluss der Motivation kontrolliert.
Beispieldatensatz für die ANCOVA in SPSS zum Download
4 Durchführung der Varianzanalyse mit Kovariaten in SPSS (ANCOVA)
4.1 Voraussetzung 1: über Gruppen hinweg homogene Kovariate
Zunächst sollte eine einfache ANOVA (ausführlich hier) gerechnet werden, um zu prüfen, ob die Kovariate über die Gruppen hinweg ähnlich sind.
Über das Menü in SPSS: Analysieren > Allgemeines lineares Modell > Univariat. Als abhängige Variable ist in dem Falle die Kovariate (im Beispiel: Motivation) zu wählen und als Fester Faktor die Gruppierungsvariable (hier: Trainingsstand).
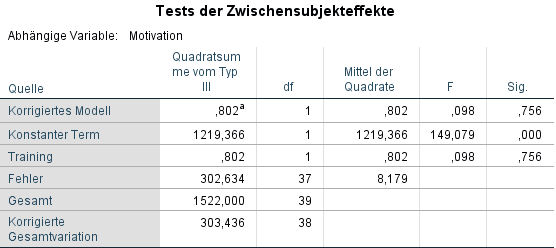
Sofern die Signifikanz über 0,05 liegt, können wir die Nullhypothese von Homogenität nicht ablehnen. Demzufolge können wir von Homogenität der Kovariaten über die Gruppen hinweg ausgehen. Oder anders ausgedrückt. Die mittlere Motivation ist in beiden Gruppen in etwa gleich, wodurch keine Verzerrung durch sie zu erwarten ist.
Im Beispiel ist die Signifikanz mit 0,756 deutlich über der Verwerfungsgrenze von Alpha=0,05. Die erste spezielle Voraussetzung für die ANCOVA ist damit erfüllt.
4.2 Voraussetzung 2: Homogenität der Regressionssteigungen
Die Kovariate und die abhängige Variable sollten eine lineare vergleichbare (homogene) Beziehung zueinander haben. Das kann über verschiedene Wege gemacht werden. Der einfachste ist ein gruppiertes Streudiagramm mit der Kovariate an der einen und der abhängigen Variablen an der anderen Achse. Wenn die Regressionsgeraden ähnlich aussehen, ist dies Voraussetzung erfüllt. Eine andere Variante zeige ich im oben verlinkten Video.
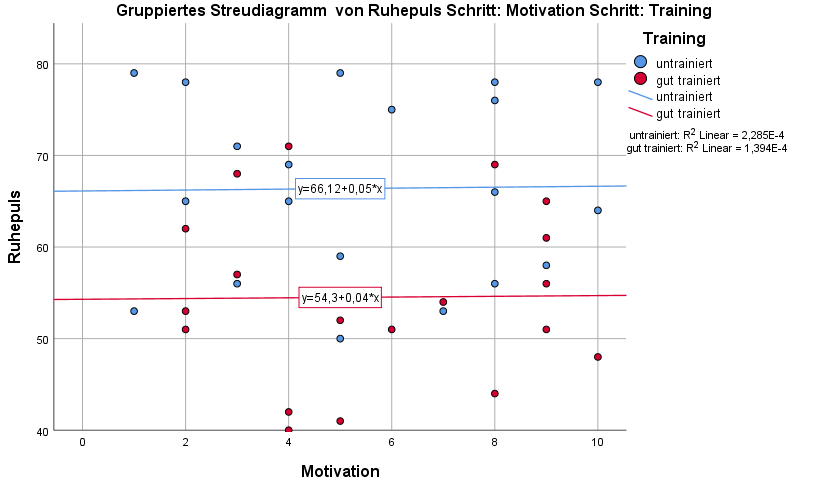
Im Beispiel sind die Regressionsgleichungen ein Zeichen für eine sehr schlechte Passung, sie sind aber aufgrund ihrer Parallelität im Verlauf her ziemlich ähnlich.
4.3 Die Berechnung der ANCOVA selbst
Über das Menü in SPSS: Analysieren > Allgemeines lineares Modell > Univariat
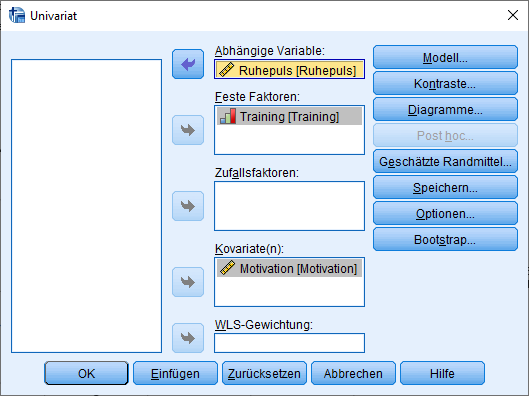
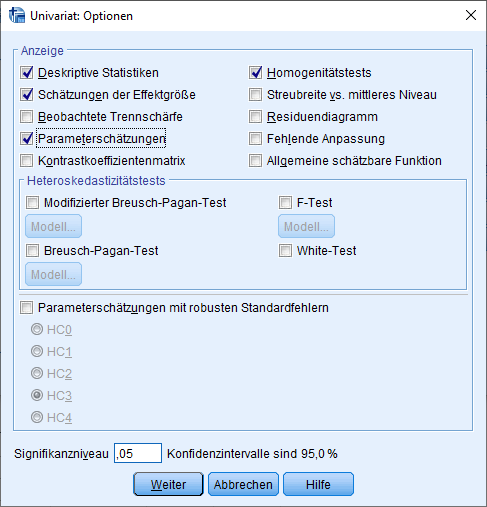
Als abhängige Variable ist die zu testende Variable hinzuzufügen (Ruhepuls), als Fester Faktor die Gruppierungsvariable (Training) und als Kovariate die Kontrollvariable (Motivation). Unter Optionen sind sinnvoll: Deskriptive Statistiken, Homogenitätstests Schätzung der Effektgröße und Parameterschätzungen. Letzteres interessiert uns insbesondere für die Effektstärke.
5 Interpretation der Ergebnisse der ANCOVA
5.1 Statistisch signifikante Effekte

Zunächst ist kurz der Levene-Test zu berichten. Er hat als Nullhypothese die Homogenität der Varianzen. Wenn die Signifikanz über 0,05 liegt, kann diese Nullhypothese nicht verworfen werden. Im Beispiel ist die Signifikanz mit 0,585 deutlich darüber, von homogenen Varianzen kann also ausgegangen werden.
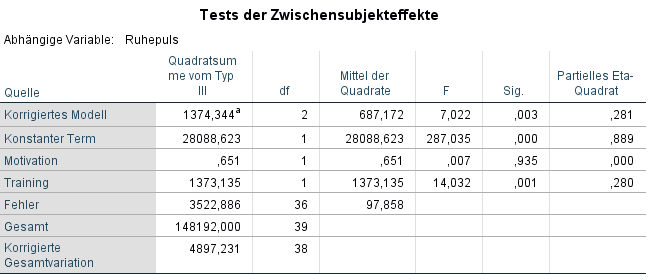
In der Tabelle “Test der Zwischensubjekteffekte” interessiert uns nun, wie das Training wirkt. Es ist mit 0,001 hoch signifikant. Die Kovariate Motivation hat hingegen mit 0,935 keinen statistisch signifikanten Einfluss auf die abhängige Variable.
5.2 Effektstärke der signifikanten Effekte
Die Effektstärke wird von SPSS nicht ausgegeben, also wie stark sich die Trainingsgruppen unterscheiden. Die ist manuell zu berechnen und mit den Grenzen Cohen: Statistical Power Analysis for the Behavioral Sciences (1988), S. 79-80 zu beurteilen. Zur Berechnung der Effektstärke des signifikanten Effektes im Rahmen der ANCOVA bedienen wir uns der r-Formel.
![Rendered by QuickLaTeX.com \[ r = \sqrt{\frac{t^2}{t^2+df}} \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-9886fca356574d85b86c73a01a18ca5b_l3.png)
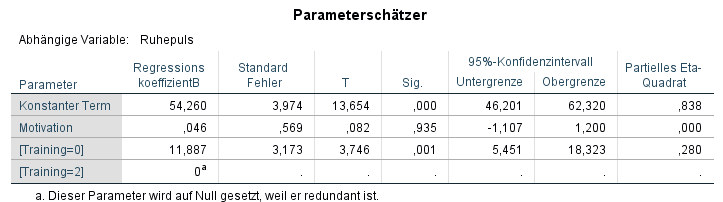
Da wir nur sinnvollerweise eine Effektstärke für einen statistisch signifikanten Effekt berechnen können, schauen wir nur in der Zeile [Training=0], weil dieser signifikant ist. Hier entnehmen wir den t-Wert 3,746. Die Freiheitsgrade (degrees of freedom, df) erhalten wir aus der Tabelle “Test der Zwischensubjekteffekte” unter “Fehler”. Im Beispiel ist es 36.
![Rendered by QuickLaTeX.com \[ r = \sqrt{\frac{3,746^2}{3,746^2+36}}=0,530 \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-5f9e32f3904b108bf04713b6bafcfadb_l3.png)
Laut Cohen (1998) ist:
- ab 0,1 schwacher Effekt,
- ab 0,25 mittlerer Effekt und
- ab 0,4 starker Effekt.
Im vorliegenden Beispiel ist der Trainingsstand mit einem r-Wert von 0,530 über der Grenze zum starken Effekt (0,4). Somit ist es ein starker Effekt.
5.3 Tipp zum Schluss
Findest du die Tabellen von SPSS hässlich? Dann schau dir mal an, wie man mit wenigen Klicks die Tabellen in SPSS im APA-Standard ausgeben lassen kann.
6 Videotutorial


